Maths & DevWeb : variable aléatoire, variance, écart-type et fonction de répartition

Lorsque l’on débute en développement web, on a souvent l’impression que les mathématiques ne serviront qu’occasionnellement, et uniquement pour quelques calculs rapides. Pourtant, dès que l’on met un pied dans l’analyse de données, l’optimisation, les probabilités ou l’IA, un nouvel univers s’ouvre. Il n’est pas nécessaire de devenir un génie des équations, mais comprendre des notions comme la variable aléatoire, la variance, l’écart-type ou la fonction de répartition change réellement la manière dont on aborde un projet.

• Comprendre comment les variables aléatoires permettent d’analyser et anticiper les comportements utilisateurs pour améliorer un site.
• Savoir interpréter variance et écart-type afin d’évaluer la stabilité, la cohérence et la fiabilité des performances web.
• Apprendre à utiliser la fonction de répartition pour repérer les seuils critiques et prendre de meilleures décisions basées sur des données réelles.

Dans ce chapitre, nous allons partir de zéro. Pas de terme technique, pas besoin d’être bon en mathématiques. Le but est que vous compreniez, vraiment, ce que représentent ces concepts. Je vous accompagnerai pas à pas, comme si vous étiez à côté de moi. Vous verrez que ces notions sont à la fois simples, utiles et même plutôt fascinantes.

Prenez votre temps et laissez-vous guider. Après tout, apprendre les mathématiques peut devenir agréable si l’on relie tout cela au développement web que vous pratiquez au quotidien.

Comprendre ce qu’est une variable aléatoire

Lorsque l’on entend le terme variable aléatoire, on a parfois l’impression de tomber sur un concept réservé aux chercheurs. Pourtant, c’est en réalité un mécanisme très simple, presque intuitif. Une variable aléatoire, c’est une variable qui peut prendre plusieurs valeurs possibles, selon un événement imprévisible.

Autrement dit, c’est comme une fonction qui transforme un événement incertain en un chiffre bien réel. En développement web, cela peut être utilisé partout où le hasard entre en jeu : génération d’un token, choix d’un utilisateur au hasard pour un test A/B, simulation d’un comportement, prédiction statistique ou même calcul de probabilités dans un jeu.

Un premier exemple très simple

Imaginez que vous vouliez coder un petit jeu en JavaScript dans lequel l’utilisateur lance un dé virtuel. Le résultat, entre 1 et 6, est imprévisible. La variable qui représente ce résultat est une variable aléatoire.

Il s’agit déjà d’une variable aléatoire au sens mathématique : elle prend plusieurs valeurs possibles, mais vous ne connaissez pas à l’avance celle qui apparaîtra. C’est exactement cela que les statistiques cherchent à analyser.

Un exemple concret en développement web

Supposons que vous analysiez combien de temps un visiteur reste sur votre site web. Une personne peut rester 10 secondes, une autre 2 minutes, une autre plus. Vous ne pouvez pas prédire la durée exacte pour la prochaine visite. Pourtant, chaque durée est une valeur mesurable.

Le temps de visite devient alors une variable aléatoire qui vous permettra d’étudier le comportement global des utilisateurs. Si vous accumulez assez de données (par exemple avec Matomo ou Google Analytics), vous pourrez ensuite calculer la durée moyenne, l’écart-type, repérer les anomalies, etc.

Lors de mon tout premier projet web en freelance, je devais analyser quelles pages fonctionnaient le mieux. Je pensais naïvement qu’un simple comptage de visite suffirait. Mais ce n’est qu’après avoir analysé la durée moyenne, la dispersion des temps de visite et quelques métriques statistiques très basiques que j’ai réellement compris comment les utilisateurs naviguaient. C’est ce genre de petit déclic qui montre pourquoi les notions que nous abordons aujourd’hui sont si importantes.

Pourquoi la variance est un outil essentiel

Maintenant que vous comprenez ce qu’est une variable aléatoire, il est temps de s’intéresser à la variance. Ce mot peut aussi sembler intimidant, mais son rôle est très clair : mesurer à quel point les valeurs d’une variable aléatoire s’éparpillent.

Pour le dire autrement, la variance représente à quel point un ensemble de données est cohérent ou, au contraire, dispersé. C’est une manière précise de savoir si des valeurs tournent autour d’une moyenne ou si elles s’en éloignent beaucoup.

Explication pas à pas

Imaginons que vous analysiez la vitesse de chargement de votre site. Vous testez dix fois votre page d’accueil.

Dans le premier cas, votre site met presque toujours autour de 900 ms à charger. Dans le deuxième, il peut charger en 400 ms… ou en 3 secondes… sans logique particulière.

Dans les deux cas, on pourrait avoir une moyenne similaire, mais le ressenti de l’utilisateur n’a rien à voir. Ce que l’on veut mesurer, c’est la régularité. C’est exactement ce que fait la variance.

Pourquoi est-ce important en développement web ?

Prenons un exemple concret. Vous proposez un formulaire sur votre site web, et vous mesurez le temps entre le moment où un utilisateur clique sur “Envoyer” et celui où votre serveur répond. Si votre serveur met :

• toujours à peu près 200 ms → expérience fluide
• parfois 50 ms, parfois 900 ms → expérience instable
• parfois 50 ms, parfois 5 secondes → expérience catastrophique

Même si la moyenne est correcte, la variance sera élevée si les temps sont très différents les uns des autres.

Cela vous permet de repérer des problèmes invisibles à travers une simple moyenne. Une variance élevée peut signifier :

• un serveur surchargé
• un problème de base de données
• des fichiers trop lourds
• un goulot d’étranglement dans une API

Comment calcule-t-on la variance ?

Pour rester accessible, je vais vulgariser le calcul sans entrer dans les formules complexes.

L’idée est simple. On veut mesurer à quel point chaque valeur s’éloigne de la moyenne. On calcule donc l’écart de chaque valeur par rapport à la moyenne, puis on élève cet écart au carré, puis on en fait la moyenne.

Pourquoi mettre au carré ? Tout simplement pour éviter que les écarts positifs et négatifs s’annulent et donnent un fausse impression de régularité.

Si vous aimez comprendre la logique :

Un écart au carré amplifie les valeurs très éloignées, ce qui permet de repérer les anomalies.

Pour simplifier son calcul, nous utiliserons la formule :

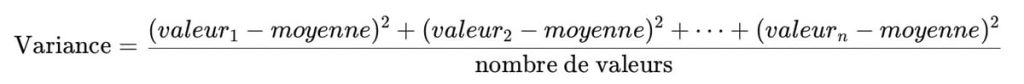
Exemple simple

Temps de chargement mesurés, en secondes :

1, 1, 1, 1, 1

La moyenne est 1. Tous les temps sont identiques. La variance est donc 0. Rien ne s’éparpille.

Autre série :

1, 3, 1, 5, 2

La moyenne est environ 2,4.
Les valeurs bougent beaucoup plus autour de la moyenne. La variance est donc bien plus élevée. Même sans calcul, vous le sentez : c’est instable.

L’écart-type : le frère jumeau de la variance, mais plus intuitif

Si la variance mesure la dispersion, l’écart-type en est simplement la version plus lisible. En effet, l’écart-type est la racine carrée de la variance. Il permet d’avoir une mesure exprimée dans les mêmes unités que les valeurs initiales.

C’est ce qui le rend plus intuitif.

Pourquoi s’en préoccuper ?

Imaginons que vous analysiez encore la vitesse de votre site. Si la variance vous dit que les temps sont très dispersés, l’écart-type vous dira à quel point ils s’écartent de la moyenne, mais dans des unités compréhensibles.

Par exemple, si votre moyenne est de 800 ms et votre écart-type est de 50 ms, vous savez que la plupart des chargements tournent entre 750 et 850 ms. C’est rassurant et facile à interpréter.

Quand l’écart-type devient un outil puissant

Dans l’analyse de données web, l’écart-type permet de :

• repérer les valeurs anormales
• estimer la fiabilité d’indicateurs
• surveiller la stabilité d’un serveur
• comprendre la régularité des comportements utilisateurs
• améliorer des modèles prédictifs
• optimiser des systèmes d’IA ou des algorithmes

L’écart-type est tellement utilisé que vous le croiserez partout : dans les dashboards analytics, dans les systèmes de scoring, dans les outils de machine learning… ou même dans les tests A/B pour mesurer la différence entre deux versions d’un site.

Exemple concret

Temps d’attente entre demande API et réponse :

300 ms en moyenne
écart-type : 40 ms

Cela signifie que vos temps tournent très souvent entre 260 et 340 ms.
On peut considérer que le service est stable.

Autre exemple :

même moyenne, mais écart-type de 180 ms

Là, vos temps varient énormément. Vous ne pouvez pas faire confiance à cette API. Elle peut marcher, comme elle peut bloquer un utilisateur pendant une seconde. Rien n’est prévisible.

La fonction de répartition : un outil discret mais incontournable

Après avoir exploré la variable aléatoire, la variance et l’écart-type, il est temps d’aborder un concept un peu moins connu mais pourtant essentiel : la fonction de répartition cumulée. Ne vous laissez pas impressionner par ce nom. Cette fonction, que l’on surnomme souvent F(x), répond à une question toute simple :

« Quelle est la probabilité que ma variable aléatoire soit inférieure ou égale à une certaine valeur ? »

Autrement dit, elle permet de regarder l’ensemble des résultats possibles et de savoir à quel point un événement est courant ou rare. Cela devient très utile lorsqu’on veut analyser des données, anticiper des comportements ou estimer un risque.

Comment créer une fonction de répartition cumulée

Pour construire une fonction de répartition cumulée, l’idée est vraiment simple : vous allez regarder, pour chaque nombre possible, quelle proportion de vos valeurs sont inférieures ou égales à ce nombre.

Concrètement, vous commencez par trier vos données du plus petit au plus grand. Ensuite, pour chaque valeur du tableau, vous comptez combien de valeurs sont en dessous ou égales à elle, puis vous divisez ce nombre par le total de valeurs.

Des formations informatique pour tous !

Débutant ou curieux ? Apprenez le développement web, le référencement, le webmarketing, la bureautique, à maîtriser vos appareils Apple et bien plus encore…

Formateur indépendant, professionnel du web depuis 2006, je vous accompagne pas à pas et en cours particulier, que vous soyez débutant ou que vous souhaitiez progresser. En visio, à votre rythme, et toujours avec pédagogie.

Découvrez mes formations Qui suis-je ?

Cela vous donne un pourcentage qui augmente progressivement jusqu’à 100 %. En reliant ces points sur un graphique, vous obtenez une courbe en forme de S, qui montre à quel endroit se concentrent la majorité de vos données.

On note généralement la fonction de répartition cumulée par F(x).

La formule est :

F(x) = P(X≤x)

En mots simples :
F(x) représente la probabilité que la valeur de votre variable soit plus petite ou égale à x.

Si vous préférez une forme « à la main », sans symbole compliqué :

F(x) = (nombre de valeurs ≤ x) / nombre total de valeurs

C’est tout. Rien d’autre.

Imaginons que vous ayez mesuré le temps (en secondes) que 5 personnes ont passé sur une page web :

3, 5, 8, 10, 12

Déjà, on trie (ici c’est déjà trié). Maintenant, imaginons qu’on veut calculer F(8).
Cela veut dire : « Quelle proportion de personnes sont restées 8 secondes ou moins ? »

On compte :

• 3 ≤ 8 → oui
• 5 ≤ 8 → oui
• 8 ≤ 8 → oui
• 10 ≤ 8 → non
• 12 ≤ 8 → non

Il y a 3 valeurs ≤ 8, sur 5 valeurs au total.

On applique la formule simple :

F(8) = 3 / 5 = 0,6

Donc F(8) = 0,6.
Avec des mots simples : 60 % des visiteurs restent au moins 8 secondes.

Explication intuitive

Visualisez une courbe qui monte doucement, jamais brutalement, et qui ne descend jamais. Au début, elle démarre à zéro. À la fin, elle finit à un. Cette courbe est la fonction de répartition.

Pourquoi finit-elle à un ? Parce que 1 représente la probabilité totale, soit cent pour cent des cas.

À quoi cela sert ? À faire des prédictions simples !

Par exemple, si vous analysez les temps de visite sur crea-troyes.fr et que votre fonction de répartition vous dit que F(30 secondes) = 0.40, cela signifie qu’environ 40 pour cent des visiteurs quittent la page avant la trentième seconde. C’est une information précieuse pour optimiser vos contenus, vos appels à l’action ou votre design.

Exemple concret pour bien comprendre

Supposons que vous mesuriez la durée de consultation d’un article de tutoriel. Vous notez des durées aléatoires : certaines de deux minutes, d’autres de trente secondes, quelques-unes de sept minutes. Après avoir constitué vos données, vous pouvez construire la fonction F(x).

Si vous obtenez F(60 secondes) = 0,55, cela signifie que plus de la moitié de vos visiteurs partent avant une minute. Vous n’avez alors plus besoin de réfléchir à l’aveugle pour optimiser votre contenu : vous savez précisément que vos premiers paragraphes doivent attirer, captiver, expliquer ou intriguer.

À l’inverse, si F(120 secondes) = 0,80, cela veut dire que quatre lecteurs sur cinq partent avant deux minutes. C’est une mine d’informations pour ajuster votre stratégie éditoriale.

Un lien direct avec l’écart-type

La fonction de répartition permet aussi de visualiser si une distribution est très étalée (grande variance) ou assez resserrée (écart-type faible). Si la courbe monte rapidement, cela signifie que la plupart des gens ont un comportement similaire. Si elle monte lentement, c’est que les comportements sont très hétérogènes.

En développement web, cette distinction est capitale, car elle vous indique si vos visiteurs agissent de manière prévisible ou non.

Relier ces notions au développement web moderne

Maintenant que vous connaissez les bases, je voudrais vous montrer comment ces concepts s’articulent dans des situations réelles que vous rencontrerez en développement web, dans vos projets personnels ou même au sein de votre entreprise.

Optimiser la performance d’un site

Les variables aléatoires sont au cœur de toutes les mesures de performance. Lorsque vous utilisez un outil comme Lighthouse ou GTmetrix, chaque test de performance vous renvoie un temps de chargement. Ces temps sont des valeurs d’une variable aléatoire.

• La variance vous indique si vos performances sont régulières ou instables.
• L’écart-type donne une idée précise de l’ampleur de ces variations.
• La fonction de répartition vous apprend à quel point des temps très longs sont fréquents.

En pratique, cela vous aide à décider s’il faut optimiser vos images, revoir vos requêtes SQL ou migrer vers un meilleur hébergement.

Comprendre les comportements utilisateurs

Les analystes web utilisent constamment ces notions. Par exemple : Durée de visite, nombre de pages consultées, temps entre deux clics, taux de rebond, durée avant abandon d’un formulaire. Tout cela forme des variables aléatoires.

Si vous calculez la variance du temps passé sur une page, vous pouvez deviner si la page intéresse principalement un type d’utilisateur précis ou si elle plaît à tout le monde.

Si vous calculez la fonction F(x), vous découvrez précisément combien de minutes un lecteur consacre à votre contenu avant de décrocher. C’est comme regarder vos utilisateurs naviguer… mais sans être derrière eux.

Améliorer un système de recommandation ou de scoring

Si un jour vous implémentez un système de recommandation sur code.crea-troyes.fr (par exemple pour suggérer des exercices adaptés au niveau de l’utilisateur), vous aurez besoin de probabilités et de statistiques. Les écarts-types, les variances, les distributions… tout cela sert à comprendre comment les utilisateurs progressent, réussissent des quizz ou abandonnent certaines missions.

Même sans viser de l’IA avancée, ces notions deviennent des outils pour mieux orienter vos décisions.

Exemple de A à Z

Afin de rassembler les différentes notions, je vous propose une expérience très simple que vous pourriez coder si vous le souhaitez. Elle n’a rien de scientifique, mais permet de visualiser le rôle de chaque concept.

Prenons une variable aléatoire X : le temps (en secondes) que met un utilisateur pour remplir un petit quiz de trois questions dans votre futur site web.

Vous faites passer ce quiz à 20 testeurs. Vous obtenez des temps variés : certains répondent en 20 secondes, d’autres en 45, un ou deux ont fait traîner jusqu’à une minute et demie.

Première étape : calculer la moyenne. Cela vous donne un temps typique.

Deuxième étape : calculer la variance. Vous découvrez alors si vos testeurs ont un profil homogène ou très hétérogène.

Troisième étape : calculer l’écart-type. Cela vous permet de mesurer précisément la dispersion, avec les mêmes unités que votre variable. Ainsi, vous pouvez dire par exemple que la plupart des testeurs sont à plus ou moins 12 secondes autour de la moyenne.

Dernière étape : tracer la fonction de répartition F(x). Avec elle, vous pouvez répondre à des questions pratiques :

• « Quelle proportion des testeurs terminent le quiz en moins de 40 secondes ? »
• « Beaucoup mettent-ils plus d’une minute ? »
• « Le quiz est-il trop difficile ? »

En quelques minutes d’analyse, vous obtenez une vision claire pour ajuster votre quiz avant la mise en ligne publique.

Quand les mathématiques deviennent un atout pour le développeur

Il peut être tentant de repousser les statistiques en pensant que ce n’est pas indispensable en développement web. Pourtant, même sans faire de recherche mathématique, cette compréhension vous donne un avantage. Vous pouvez analyser vos données de manière intelligente, comprendre les comportements, anticiper les besoins et améliorer vos interfaces avec une précision que seule l’analyse statistique permet.

J’ai rencontré un développeur lors d’un atelier qui m’a confié qu’il n’avait jamais aimé les mathématiques jusqu’à ce qu’il réalise que chaque mesure sur un site reflétait une histoire utilisateur. En visualisant les nombres comme des comportements et non comme des abstractions, il avait découvert un nouvel intérêt. C’est un peu l’esprit de ce chapitre : vous montrer que ces notions servent avant tout à mieux comprendre la réalité.

Vous venez de parcourir un ensemble de notions qui peuvent paraître impressionnantes lorsque l’on débute, mais qui sont en réalité beaucoup plus accessibles qu’on ne l’imagine dès que l’on prend le temps de les relier au concret. Les variables aléatoires, la variance, l’écart-type et les fonctions de répartition sont avant tout des outils pour éclairer des situations réelles, des comportements, des performances ou des données qui se présentent quotidiennement dans vos projets web.

Vous découvrirez rapidement que ces connaissances vous servent plus souvent que prévu. Que vous souhaitiez optimiser un site, analyser les visites, ajuster un système de quizz ou comprendre pourquoi un serveur se comporte de manière instable, ces notions vous guideront. Elles constituent une base solide, et vous n’avez pas besoin de devenir un expert en statistiques pour les utiliser intelligemment.

Gardez surtout une idée importante en tête : la statistique n’est pas une montagne infranchissable. C’est un ensemble d’outils concrets, logiques et souvent très intuitifs. Si vous continuez à explorer ces concepts, vous serez surpris de voir à quel point ils s’intègrent naturellement dans votre travail de développeur et combien ils peuvent soutenir vos décisions.

Alban

Fondateur de l’agence Créa-troyes, affiliée France Num
Intervenant en Freelance.
Contactez-moi

crea-troyes.fr