Loi binomiale : Un pilier des maths et du développement web

Lorsque l’on commence à coder des fonctionnalités un peu plus poussées dans le développement web, on tombe parfois sur des calculs qui semblent mystérieux. Probabilités, statistiques, prédictions, tests A/B… Tout cela paraît souvent réservé à ceux qui ont adoré les maths au lycée. Mais la vérité est beaucoup plus simple. Il existe une poignée de notions qui, une fois bien comprises, ouvrent un champ d’application immense. Parmi elles, la loi binomiale.

• Comprendre clairement la loi binomiale pour enfin interpréter des situations de réussite/échec répétées sans être perdu face aux probabilités.
• Savoir appliquer la loi binomiale pour analyser des données réelles comme les conversions, les clics ou les tests A/B, et prendre de meilleures décisions.
• Être capable de calculer et utiliser la loi binomiale en JavaScript ou PHP afin d’intégrer ces notions directement dans ses projets web.

La surprenante force de la loi binomiale est de permettre de répondre à une question que l’on se pose souvent dans la vie de tous les jours, mais aussi dans le web : si j’ai un événement qui peut réussir ou échouer, combien de fois ai-je des chances de réussir ? Et avec quelle probabilité ? Derrière ces interrogations assez banales se cache un outil puissant, totalement accessible, même si vous pensez ne « rien comprendre » aux maths.

Dans cechapitre complet, nous allons partir de zéro. Pas d’équations jetées au visage sans explication. Nous allons avancer pas à pas, avec des exemples concrets, y compris ceux que vous pouvez rencontrer dans le monde du développement web. Et promis, à la fin, vous aurez non seulement compris le concept, mais vous saurez l’appliquer vous-même.

Comprendre la loi binomiale

Pour comprendre la loi binomiale, imaginez que vous faites une action simple, qui n’a que deux issues possibles. Par exemple gagner ou perdre, cliquer ou ne pas cliquer, réussir ou échouer. Les maths appellent cela une épreuve de Bernoulli. Rien de magique : c’est simplement un événement à deux résultats possibles.

L’Épreuve de Bernoulli en bref

Une épreuve de Bernoulli est l’expérience aléatoire la plus simple qui existe. Sa particularité est qu’elle ne possède que deux issues possibles : soit cela fonctionne, soit cela ne fonctionne pas. Il n’y a pas de milieu. En mathématiques, on nomme ces deux résultats :

• Le Succès : C’est le résultat que l’on recherche (par exemple : « obtenir un 6 avec un dé »).
• L’Échec : C’est tout le reste (par exemple : « faire 1, 2, 3, 4 ou 5 »).

C’est une logique booléenne. On retrouve ce même principe en développement web et en programmation avec les fameux :

• True
• False

L’exemple du « Pile ou Face » : Pour bien comprendre, imaginez que vous lancez une pièce de monnaie.

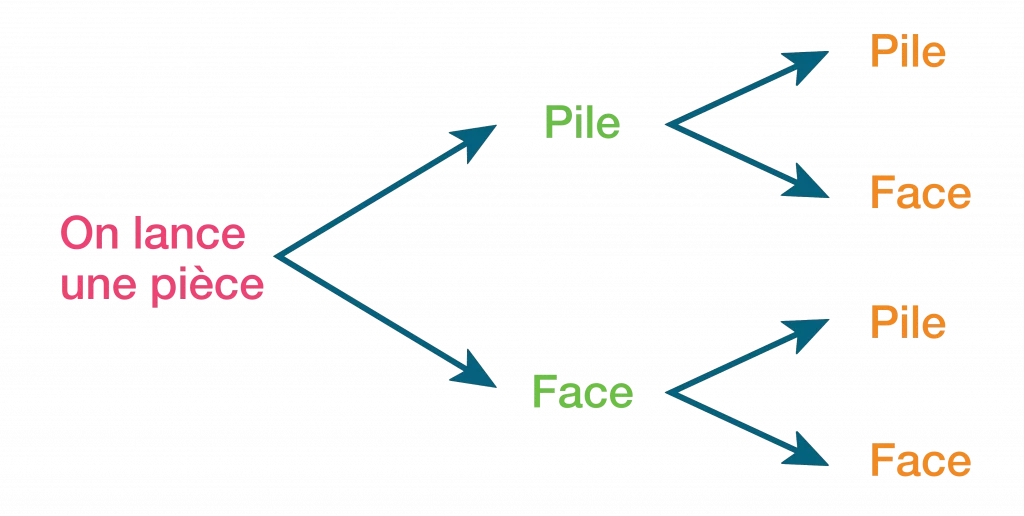
C’est l’exemple parfait d’une épreuve de Bernoulli car :

1. C’est du hasard (on ne sait pas sur quoi elle va tomber).
2. Il n’y a que deux options : Pile ou Face (la pièce ne peut pas rester en l’air ou tomber sur la tranche).

Si vous décidez que votre but est d’avoir « Pile », alors :

• Tomber sur Pile est le Succès.
• Tomber sur Face est l’Échec.

C’est tout simplement ça : une question de hasard à laquelle on ne peut répondre que par « Oui » ou par « Non ».

L’idée clé : répéter plusieurs fois un événement simple

La loi binomiale intervient lorsque vous répétez cette même épreuve plusieurs fois dans les mêmes conditions. Pour que cela fonctionne, trois éléments doivent être réunis.

Le premier, c’est que l’événement doit avoir seulement deux résultats possibles. Le second, c’est que chaque répétition doit avoir la même probabilité de réussite. Le troisième, c’est que ces répétitions doivent être indépendantes : ce qui se passe à un instant donné n’influence pas la suite.

Cette configuration, vous la croisez partout, même sans le savoir. Vous la retrouvez dans les statistiques marketing, dans la modélisation d’un taux de clic, dans l’analyse de conversions ou de paniers d’achat, et même dans les mini-jeux que l’on code pour s’entraîner.

Le concept est né il y a plus de trois siècles. Jacob Bernoulli, mathématicien suisse, avait été tellement fasciné par ces répétitions d’expériences qu’il a passé 20 ans de sa vie à les étudier avant de publier ses résultats. Imaginez consacrer deux décennies à une pièce de monnaie… C’est probablement l’exemple le plus solide de persévérance mathématique.

Un premier exemple simple et concret

Prenons un cas que tout le monde visualise facilement : lancer une pièce. Elle a deux réponses possibles : pile ou face. La probabilité d’obtenir pile est de 1 chance sur 2.

Supposons maintenant que vous lancez la pièce dix fois. La loi binomiale permet de répondre à une question très précise : quelle est la probabilité d’obtenir exactement 6 piles sur les 10 lancers ?

Et c’est là que l’on découvre son utilité : elle quantifie précisément ces situations où l’on répète un événement simple.

La formule de la loi binomiale

La loi binomiale s’écrit de manière assez élégante :

P(X = k) = C(n, k) × p^k × (1 − p)^(n − k)

À première vue, cela peut sembler intimidant. Pourtant, chaque morceau est logique et facile à comprendre lorsque l’on prend le temps de le décortiquer.

• n représente le nombre total d’essais. Si vous lancez une pièce 10 fois, n = 10.
• k est le nombre de réussites que vous voulez mesurer. Par exemple, obtenir 6 piles.
• p est la probabilité de réussite à chaque essai. Pour une pièce équilibrée, p = 0,5.
• C(n, k) est ce qu’on appelle une combinaison. En termes simples, cela indique combien de façons différentes il existe d’obtenir k réussites parmi n essais.

Prenons le temps de détailler cette combinaison.

Le rôle des combinaisons dans la loi binomiale

Reprenons notre exemple de pièce. Obtenir 6 piles sur 10 lancers peut arriver de nombreuses manières différentes. Vous pouvez avoir les 6 premiers lancers qui donnent pile, puis 4 faces. Ou la pile peut apparaître de manière plus dispersée, par exemple aux positions 2, 3, 5, 6, 8 et 9.

Pourquoi parle-t-on de combinaison ?

Ces deux résultats sont différents, mais ils comptent comme une seule même situation : 6 piles sur 10.

Chaque fois que vous changez l’ordre d’apparition des piles et des faces, cela crée une configuration différente. Le rôle de la combinaison est donc de compter ces configurations possibles.

La formule complète de C(n, k) n’a rien d’obligatoire à retenir pour comprendre l’idée. Mais, si vous y tenez, la voici :

C(n, k) = n! / (k! × (n − k)!)

Mais ce qui compte surtout, c’est son sens : compter les façons d’obtenir un certain nombre de réussites.

Exemple concret d’une combinaison

Imaginez que vous avez 4 tentatives, et que vous voulez savoir combien de façons il existe d’obtenir 2 réussites.

Vous pouvez avoir réussite-réussite-échec-échec, ou réussite-échec-réussite-échec, ou encore échec-réussite-échec-réussite.
Il y en a exactement 6.

Dans ce cas, C(4, 2) = 6.

Ces combinaisons se retrouvent ensuite multipliées par les probabilités de réussite et d’échec, selon leur nombre. C’est pour cela que l’ensemble fonctionne parfaitement pour modéliser une séquence d’événements répétitifs.

Interpréter la loi binomiale dans le monde du développement web

Vous pourriez vous demander : en tant que développeur web, à quoi cela peut-il bien me servir ? À vrai dire, beaucoup plus souvent que vous ne l’imaginez.

Le taux de clic (CTR)

Supposons que vous travaillez sur un site, par exemple votre blog, ou un projet client. Vous analysez un bouton d’appel à l’action. D’après vos statistiques, un visiteur sur dix clique sur ce bouton. On estime donc que la probabilité de clic, p, vaut 0,1.

La question devient : si 100 visiteurs consultent la page aujourd’hui, combien de clics avez-vous des chances d’obtenir ?

La loi binomiale permet de répondre à : quelle est la probabilité d’obtenir exactement 8 clics, ou au moins 15 clics, ou moins de 5 clics ?

Ce n’est pas seulement de la curiosité mathématique. C’est ce qui permet de comprendre la variabilité naturelle du trafic, d’évaluer si vos résultats sont normaux ou surprenants, et même de justifier des décisions auprès d’un client.

Les tests A/B

Vous comparez deux versions d’une page : la A et la B. En apparence, vous observez un écart de performance. Mais est-ce un écart réel ou simplement le fruit du hasard ?

Les plateformes d’analytics utilisent la loi binomiale (ou ses dérivés) pour détecter si une différence de conversion est significative. Comprendre les bases vous donne un œil beaucoup plus avisé sur les résultats de vos campagnes.

En savoir plus sur Le A/B Testing.

Les jeux et fonctionnalités interactives

Un autre domaine où les développeurs web appliquent la loi binomiale sans s’en rendre compte, c’est dans les mini-jeux, les simulateurs, les générateurs de hasard, les fonctionnalités ludiques.

Par exemple, une mécanique où un personnage a 30% de chances de réussir une action, et vous voulez simuler cela sur plusieurs tentatives. La loi binomiale donne une modélisation parfaitement adaptée.

Illustration avec un exemple complet

Prenons une situation très réaliste : vous avez une landing page. Vous savez que le taux de conversion moyen est de 5%.

Vous recevez 50 visiteurs. Vous voulez savoir quelle est la probabilité d’obtenir exactement 3 conversions.

Dans ce cas :

• n = 50
• k = 3
• p = 0,05

On applique la formule.

Des formations informatique pour tous !

Débutant ou curieux ? Apprenez le développement web, le référencement, le webmarketing, la bureautique, à maîtriser vos appareils Apple et bien plus encore…

Formateur indépendant, professionnel du web depuis 2006, je vous accompagne pas à pas et en cours particulier, que vous soyez débutant ou que vous souhaitiez progresser. En visio, à votre rythme, et toujours avec pédagogie.

Découvrez mes formations Qui suis-je ?

C(50, 3) × (0,05)^3 × (0,95)^47

Ce calcul peut sembler long à faire à la main. Heureusement, en développement web, on ne fait jamais ce type de calcul « manuellement ». On le délègue à une fonction, à une bibliothèque, ou à un petit script maison.

Mais comprendre ce que vous calculez reste fondamental pour ne pas voir les chiffres comme un brouillard incompréhensible.

Calculer la loi binomiale pas à pas

Maintenant que les bases sont en place, il est temps de passer à l’application. C’est souvent le moment où les débutants se crispent, persuadés que les maths vont redevenir abstraites. Mais rassurez-vous : une fois que vous avez compris ce que signifient n, k, p et les combinaisons, le calcul devient presque mécanique.

Imaginez que vous deviez l’expliquer à un ami autour d’un café. Le processus tient en trois étapes simples.

D’abord vous calculez le nombre de combinaisons possibles. Ensuite vous calculez la probabilité d’obtenir k réussites. Puis celle d’obtenir les échecs restants. Enfin, vous multipliez tout. Cela paraît long dit comme ça, mais en pratique, cela se déroule naturellement.

Pour illustrer, reprenons un exemple clair. Supposons que vous développez une application de sondage. Chaque utilisateur a 70% de chance de répondre à une question facultative. Vous obtenez 12 utilisateurs. Vous voulez connaître la probabilité d’avoir exactement 9 réponses.

Vous identifiez n = 12, k = 9 et p = 0,7.

1. La première étape est donc de déterminer C(12, 9). Cela revient à compter toutes les manières possibles de choisir 9 utilisateurs qui répondent parmi 12.
2. Puis vous calculez p^k, c’est-à-dire 0,7^9.
3. Ensuite vous calculez (1 − p)^(n − k), soit 0,3^3.
4. Il ne reste plus qu’à multiplier Combinaison × 0,7^9 × 0,3^3.

Même si les chiffres deviennent petits ou grands, le principe reste toujours identique. Ce que vous faites réellement, c’est peser toutes les possibilités qui mènent à votre résultat.

Ce type de raisonnement donne un immense pouvoir d’analyse, surtout lorsqu’on débute dans les statistiques. On ne demande plus : « Pourquoi ai-je eu 9 réponses ? ». On demande : « Quelle est la probabilité de ce résultat, compte tenu de ce que je sais ? ». Ce renversement d’approche en dit long sur la maturité analytique d’un développeur.

Calculer la loi binomiale en développement web

Dans la pratique, on n’effectue jamais tous ces calculs à la main. Internet regorge de calculateurs, mais lorsqu’on est développeur web, l’idéal est souvent d’implémenter sa propre fonction. Non seulement cela garantit plus de flexibilité, mais cela permet surtout d’intégrer la loi binomiale dans ses projets : simulateurs, tests probabilistes, outils internes, analyse de données, etc.

Je vais vous montrer deux implémentations : une en JavaScript et une en PHP. Les deux suivent exactement le même raisonnement.

Implémentation JavaScript

JavaScript est parfait pour illustrer la loi binomiale, puisqu’on peut directement intégrer ce type de calcul dans une interface web, un outil maison, ou même un tableau de bord.

Voici une fonction simple qui calcule la combinaison C(n, k). Elle utilise une approche élégante qui évite les grands nombres intermédiaires, ce qui améliore la stabilité du calcul.

function combinaison(n, k) {
    let result = 1;
    for (let i = 1; i <= k; i++) {
        result = result * (n - (k - i)) / i;
    }
    return result;
}

Ensuite, vous pouvez écrire une fonction qui applique la loi binomiale directement :

function loiBinomiale(n, k, p) {
    const c = combinaison(n, k);
    return c * Math.pow(p, k) * Math.pow(1 - p, n - k);
}

Cette fonction renvoie la probabilité exacte d’obtenir k réussites sur n essais.

Par exemple :

console.log(loiBinomiale(10, 6, 0.5));

Vous obtenez ainsi la probabilité d’obtenir 6 piles sur 10 lancers.

L’avantage de JavaScript, c’est qu’il vous permet ensuite d’aller plus loin : générer un graphique, afficher une distribution complète, comparer deux scénarios, ou créer une interface pédagogique que l’on pourrait très bien publier sur notre Créa-Blog.

Implémentation en PHP

PHP, de son côté, reste incontournable pour les sites dynamiques. Si vous souhaitez intégrer une simulation probabiliste dans un back-office, un tableau d’analyse ou un module statistique, la loi binomiale y trouve parfaitement sa place.

Voici une version PHP confortable à manipuler :

function combinaison($n, $k) {
    $result = 1;
    for ($i = 1; $i <= $k; $i++) {
        $result = $result * ($n - ($k - $i)) / $i;
    }
    return $result;
}

function loi_binomiale($n, $k, $p) {
    $c = combinaison($n, $k);
    return $c * pow($p, $k) * pow(1 - $p, $n - $k);
}

Et une utilisation simple :

echo loi_binomiale(50, 3, 0.05);

PHP gère très bien les petits calculs de probabilités. Pour les grands n (par exemple un trafic de plusieurs milliers d’utilisateurs), vous pourrez vous tourner vers des bibliothèques spécialisées, mais pour la majorité des usages dans le développement web, cette méthode suffit largement.

Interpréter les résultats : ce que la loi binomiale vous apprend vraiment

Beaucoup de débutants pensent que la loi binomiale est seulement un outil de calcul. En réalité, elle est bien plus riche. Elle vous apprend à mieux comprendre les variations naturelles d’un phénomène. Elle vous permet de distinguer le normal du surprenant.

Imaginons que vous observez un taux de conversion de 5%. Vous recevez 100 visiteurs aujourd’hui. Si vous obtenez 3 conversions, votre instinct pourrait vous dire : « C’est catastrophique ». Pourtant, en appliquant la loi binomiale, vous vous rendez compte que ce résultat, même s’il semble faible, reste probable. Il n’a rien d’anormal.

À l’inverse, si vous observez 18 conversions alors que vous en attendiez 5, vous pourriez être tenté de sauter de joie. Mais là encore, la loi binomiale indique si ce résultat est exceptionnel ou non. Si la probabilité de ce résultat est très faible, alors oui, vous avez vécu une journée exceptionnelle. Sinon, c’est peut-être juste la variabilité naturelle.

Cette manière de penser protège le développeur web de décisions impulsives. Elle aide à distinguer les vraies tendances des fluctuations temporaires.

Un professeur demandait chaque année à ses étudiants de simuler une suite de pile ou face sans utiliser de pièce. Ensuite, il comparait cette suite à une vraie série aléatoire. Ironie du sort : c’était toujours la série inventée par les élèves qui paraissait moins chaotique. La loi binomiale explique précisément pourquoi : nous sous-estimons instinctivement les fluctuations naturelles.

Exemple approfondi : une distribution complète

Pour mieux comprendre, prenons un scénario très concret pour un développeur web. Vous gérez une newsletter. D’après vos statistiques, 30% des abonnés ouvrent vos emails. C’est p = 0,3. Vous envoyez une newsletter à un échantillon de 20 personnes, soit n = 20.

Vous pourriez vouloir connaître la probabilité de différentes valeurs :

• la probabilité d’avoir 5 ouvertures
• la probabilité d’avoir 10 ouvertures
• la probabilité d’avoir entre 4 et 8 ouvertures

Grâce à la loi binomiale, vous pouvez calculer chacune de ces probabilités. Et en les mettant toutes à la suite, vous obtenez ce que l’on appelle une distribution binomiale.

Cette distribution est très intéressante. Elle vous montre où se trouve la valeur la plus probable, mais aussi comment les résultats se dispersent autour de cette valeur.

Dans notre exemple :

La valeur la plus probable se situe autour de 6 ouvertures (car 0,3 × 20 = 6).
Des valeurs comme 1 ou 15 ouvertures sont possibles, mais leur probabilité est faible. Cela vous donne une intuition plus fine de ce que vous pouvez attendre lors d’un envoi classique.

Lorsque vous gérez un site web, cette capacité à interpréter vos données avec recul fait une vraie différence. Cela vous évite d’optimiser vos contenus à l’aveugle ou de tirer des conclusions trop hâtives.

Comment maîtriser la loi binomiale sans effort

Comme toute notion mathématique, la loi binomiale peut sembler lourde lorsqu’on la découvre. Pourtant, il existe trois astuces simples pour la maîtriser sans peine.

La première est de toujours revenir à ce que signifie réellement l’expérience répétée. Visualisez vos n essais, vos k réussites. Même sous forme imagée, cette représentation ancre l’idée dans votre esprit.

La deuxième astuce consiste à toujours vous demander pourquoi le résultat a tel poids. Pourquoi cette configuration est-elle plus probable qu’une autre ? Pourquoi celle-ci est-elle plus rare ? Ce questionnement développe votre intuition.

La troisième, enfin, est l’application. Rien ne remplace la pratique régulière. Écrivez une petite fonction JavaScript. Créez un simulateur simple. Calculez quelques distributions pour des projets web. En manipulant la loi binomiale avec des exemples personnels, vous l’apprivoiserez plus vite que vous ne l’imaginez.

La loi binomiale n’est pas seulement un concept mathématique. C’est un véritable outil pour comprendre les phénomènes incertains qui traversent votre quotidien de développeur web. Elle vous aide à analyser vos taux de conversion, à interpréter vos statistiques, à structurer vos tests A/B ou à construire des fonctionnalités interactives crédibles.

Elle vous offre aussi une vision plus lucide du hasard. Au lieu de subir les variations de vos données, vous commencerez à les comprendre. Et comprendre, c’est toujours gagner en liberté. Vous serez capable de prendre de meilleures décisions, de mieux anticiper les tendances et de justifier plus solidement vos analyses, que ce soit sur vos projets clients ou dans n’importe quel tableau de bord.

Enfin, la loi binomiale vous montre quelque chose d’essentiel : derrière ce qui vous paraît chaotique, il existe toujours une structure. Loin d’être un mur de formules, c’est un langage qui raconte une histoire, celle de vos données. Et une fois que vous l’entendez, vous ne regardez plus vos statistiques de la même manière.

Alban

Fondateur de l’agence Créa-troyes, affiliée France Num
Intervenant en Freelance.
Contactez-moi

crea-troyes.fr