La cryptographie moderne repose sur des mathématiques complexes, souvent perçues comme un univers réservé aux experts en sécurité ou aux chercheurs. Pourtant, elle est aujourd’hui au cœur de tout ce que nous faisons sur Internet : connexion à un site, paiement en ligne, envoi d’un message chiffré ou signature électronique. Parmi les nombreuses méthodes cryptographiques existantes, une technologie se distingue par son efficacité et sa sécurité : la cryptographie à courbe elliptique, plus connue sous le nom de ECC (Elliptic Curve Cryptography).
L’objectif de ce chapitre sur la cryptographie est de vous expliquer pas à pas ce qu’est une courbe elliptique (ECC), comment elle fonctionne et pourquoi elle est aujourd’hui largement utilisée dans le monde de la sécurité informatique, notamment en cryptographie asymétrique.
Vous découvrirez également comment l’utiliser concrètement en PHP, avec des exemples simples et commentés. Ce tutoriel s’inscrit dans la continuité de notre série sur la cryptographie et servira de base solide pour comprendre des algorithmes tels que ECDSA, ECDH ou encore les certificats SSL basés sur les courbes elliptiques.
- Qu’est-ce que la cryptographie à courbe elliptique (ECC) ?
- D’où vient la cryptographie à courbe elliptique ?
- Comprendre les courbes elliptiques sans formule compliquée
- L’addition de points sur une courbe elliptique
- Le cœur de la sécurité : le logarithme discret elliptique
- Les signatures numériques avec ECC (ECDSA)
- L’échange de clés sécurisé : le protocole ECDH
- ECC et la sécurité des communications web (HTTPS)
- Les courbes les plus utilisées en cryptographie
- Comparaison ECC vs RSA : que choisir ?
- Vers l’avenir : ECC et cryptographie post-quantique
- Pourquoi comprendre l’ECC est essentiel
Qu’est-ce que la cryptographie à courbe elliptique (ECC) ?
Pour comprendre la cryptographie à courbe elliptique, il faut d’abord rappeler ce qu’est la cryptographie asymétrique. Contrairement à la cryptographie symétrique, où la même clé sert à chiffrer et à déchiffrer un message, la cryptographie asymétrique utilise deux clés distinctes : une clé publique, partagée avec tous, et une clé privée, gardée secrète par le propriétaire.
Les algorithmes RSA, DSA ou Diffie-Hellman reposent tous sur ce principe. Cependant, ils ont un inconvénient majeur : ils nécessitent des clés très longues pour garantir un haut niveau de sécurité.
C’est ici que la cryptographie à courbe elliptique entre en scène. Elle permet d’obtenir le même niveau de sécurité que RSA, mais avec des clés beaucoup plus courtes, ce qui la rend plus rapide et plus efficace.
Par exemple :
- Une clé RSA de 2048 bits offre un niveau de sécurité équivalent à
- Une clé ECC d’environ 256 bits seulement.
C’est une réduction énorme, qui a un impact direct sur les performances des serveurs, des navigateurs et des systèmes embarqués.
D’où vient la cryptographie à courbe elliptique ?
Les courbes elliptiques ont d’abord été étudiées par les mathématiciens du XVIIIe siècle dans le cadre de la géométrie et de la théorie des nombres. Ce n’est qu’au début des années 1980 que deux chercheurs, Neal Koblitz et Victor Miller, ont eu l’idée d’utiliser ces courbes dans le domaine de la cryptographie.
L’idée fondamentale est la suivante : sur une courbe elliptique, certaines opérations mathématiques (comme l’addition de points) sont faciles à effectuer, mais leur inversion est extrêmement difficile. C’est exactement le type de déséquilibre que recherche la cryptographie asymétrique.
Ainsi, la sécurité d’un système ECC repose sur la difficulté du problème du logarithme discret sur une courbe elliptique — un problème considéré comme quasi insoluble avec les moyens actuels, même pour les ordinateurs les plus puissants.
Comprendre les courbes elliptiques sans formule compliquée
Une courbe elliptique n’a rien à voir avec une ellipse. C’est une courbe mathématique définie par une équation du type :
y2 = x3+ ax + b
où a et b sont des constantes qui déterminent la forme de la courbe.
Cette courbe doit respecter une condition importante pour être « valide » en cryptographie : elle ne doit pas avoir de points singuliers (ni boucles, ni croisements).
Cette condition s’écrit ainsi :
4a3 + 27b2 ≠ 0
Visuellement, une courbe elliptique est une sorte de boucle douce et symétrique. Chaque point sur la courbe représente un couple de coordonnées (x, y).
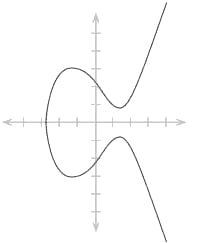
Mais alors, comment fait-on de la cryptographie avec une simple courbe ? C’est ici qu’intervient l’opération clé de l’ECC : l’addition de points.
L’addition de points sur une courbe elliptique
Sur une courbe elliptique, il existe une loi d’addition particulière entre deux points.
Si vous prenez deux points A et B sur la courbe, vous pouvez tracer une droite entre eux. Cette droite coupera la courbe en un troisième point C’. On prend alors le symétrique de ce point par rapport à l’axe des abscisses pour obtenir le point C.
Cette opération d’addition est notée ainsi :
C = A+BEt étonnamment, cette simple règle permet de définir une structure mathématique de groupe, ce qui est la base de toute cryptographie moderne.
Pour aller plus loin :
- Si l’on ajoute un point à lui-même (cas particulier où la droite devient tangente à la courbe), on obtient une opération de doublement.
- Et si l’on répète cette addition un grand nombre de fois, on obtient un point très éloigné, difficile à retrouver à l’envers.
C’est exactement cette difficulté qui assure la sécurité du chiffrement.
Le cœur de la sécurité : le logarithme discret elliptique
L’élément fondamental de la sécurité ECC repose sur le problème du logarithme discret elliptique. Imaginons :
- Un point de départ
G(appelé point générateur) connu de tous. - Un nombre secret
nchoisi par vous-même. - Vous calculez le point
Qobtenu après avoir ajoutéGà lui-mêmenfois.
On écrit cela ainsi :
Q = n×GLe point Q devient alors votre clé publique, tandis que n est votre clé privée.
La question suivante se pose : si quelqu’un connaît Q et G, peut-il retrouver n ?
En théorie, non. Cette opération est unilatérale : il est facile de calculer Q à partir de n, mais pratiquement impossible de retrouver n à partir de Q. C’est cette asymétrie qui rend la cryptographie à courbe elliptique si puissante.
Exemple simplifié avec un petit script PHP
Avant d’aller plus loin, voyons comment cela se traduit concrètement en PHP.
PHP ne permet pas de manipuler directement des courbes elliptiques « à la main » (sauf via des bibliothèques spécialisées), mais nous pouvons illustrer le concept avec l’extension OpenSSL, qui gère nativement les clés ECC.
Voici un exemple pour générer une paire de clés ECC :

Des formations informatique pour tous !
Débutant ou curieux ? Apprenez le développement web, le référencement, le webmarketing, la bureautique, à maîtriser vos appareils Apple et bien plus encore…
Formateur indépendant, professionnel du web depuis 2006, je vous accompagne pas à pas et en cours particulier, que vous soyez débutant ou que vous souhaitiez progresser. En visio, à votre rythme, et toujours avec pédagogie.
Découvrez mes formations Qui suis-je ?<?php
// Génération d'une paire de clés ECC avec OpenSSL
$config = [
"private_key_type" => OPENSSL_KEYTYPE_EC,
"curve_name" => "prime256v1" // Courbe utilisée
];
$resource = openssl_pkey_new($config);
// Extraction des clés
openssl_pkey_export($resource, $privateKey);
$publicKeyDetails = openssl_pkey_get_details($resource);
$publicKey = $publicKeyDetails["key"];
echo "Clé privée : \n" . $privateKey . "\n";
echo "Clé publique : \n" . $publicKey . "\n";Ce petit script génère :
- Une clé privée ECC (que vous gardez secrète)
- Une clé publique ECC (que vous pouvez partager)
Le paramètre "prime256v1" désigne une courbe elliptique standardisée, très utilisée dans les certificats SSL et les signatures électroniques.
Pourquoi les courbes elliptiques sont-elles si populaires ?
La principale raison est l’efficacité. Avec des clés plus petites et des calculs plus rapides, ECC offre une meilleure sécurité pour un coût de calcul plus faible.
Quelques avantages concrets :
- Performances accrues : les opérations ECC sont rapides, même sur des serveurs modestes.
- Faible consommation : idéal pour les objets connectés, smartphones ou systèmes embarqués.
- Sécurité équivalente à RSA, mais avec des clés beaucoup plus légères.
C’est pourquoi de nombreux protocoles modernes — TLS 1.3, Signal, Bitcoin, SSH, JWT, etc. — s’appuient aujourd’hui sur la cryptographie à courbe elliptique.
Les signatures numériques avec ECC (ECDSA)
Une des utilisations les plus courantes de la cryptographie à courbe elliptique est la signature numérique. Cette signature permet de garantir qu’un message :
- provient bien de l’expéditeur prétendu (authenticité),
- n’a pas été modifié pendant le transport (intégrité),
- et ne peut pas être renié par son auteur (non-répudiation).
Le protocole le plus connu dans ce domaine s’appelle ECDSA, pour Elliptic Curve Digital Signature Algorithm. Il est l’équivalent elliptique du DSA classique, mais bien plus performant.
Comment cela fonctionne ?
Le principe est simple à comprendre :
- L’expéditeur possède une clé privée ECC.
- Il génère une signature à partir du message qu’il souhaite envoyer.
- Le destinataire, qui possède la clé publique, peut vérifier la signature.
Ainsi, si le message ou la signature est modifié, la vérification échoue.
Exemple pratique en PHP
Voici un exemple concret de signature et de vérification d’un message avec ECC grâce à l’extension OpenSSL.
<?php
// Création d'une paire de clés ECC
$config = [
"private_key_type" => OPENSSL_KEYTYPE_EC,
"curve_name" => "prime256v1"
];
$resource = openssl_pkey_new($config);
openssl_pkey_export($resource, $privateKey);
$publicKeyDetails = openssl_pkey_get_details($resource);
$publicKey = $publicKeyDetails["key"];
// Message à signer
$message = "Ceci est un message important.";
// Signature du message
openssl_sign($message, $signature, $privateKey, OPENSSL_ALGO_SHA256);
echo "Signature (base64) : " . base64_encode($signature) . "\n";
// Vérification de la signature
$ok = openssl_verify($message, $signature, $publicKey, OPENSSL_ALGO_SHA256);
if ($ok === 1) {
echo "Signature valide";
} elseif ($ok === 0) {
echo "Signature invalide";
} else {
echo "Erreur lors de la vérification";
}Explications
- La fonction
openssl_sign()signe le message à l’aide de la clé privée. - La fonction
openssl_verify()vérifie la signature à l’aide de la clé publique. - L’algorithme SHA-256 est utilisé pour hacher le message avant signature.
Ce code illustre parfaitement le fonctionnement d’une signature numérique basée sur une courbe elliptique (ECC) : rapide, compacte et hautement sécurisée.
L’échange de clés sécurisé : le protocole ECDH
Un autre pilier fondamental de la cryptographie moderne est l’échange de clés. Dans un échange classique, deux parties (appelons-les Alice et Bob) souhaitent établir une clé secrète commune pour chiffrer leurs communications. Mais comment peuvent-ils y parvenir sans qu’un espion (appelé Eve) ne découvre la clé pendant le transfert ?
C’est le rôle du protocole Diffie-Hellman, et sa version elliptique est appelée ECDH (Elliptic Curve Diffie-Hellman).
Principe du protocole ECDH
- Alice et Bob choisissent une courbe elliptique et un point générateur G.
- Alice génère un secret privé
aet calcule sa clé publiqueA = a × G. - Bob fait de même avec
bet calculeB = b × G. - Alice reçoit
Bet calculeS = a × B. - Bob reçoit
Aet calculeS = b × A.
Les deux obtiennent alors le même point S sur la courbe elliptique, sans jamais avoir échangé leur clé privée. Ce point peut servir à dériver une clé de chiffrement symétrique commune.
Simulation simple en PHP
<?php
// Génération des clés ECC pour Alice
$config = ["private_key_type" => OPENSSL_KEYTYPE_EC, "curve_name" => "prime256v1"];
$alice = openssl_pkey_new($config);
openssl_pkey_export($alice, $alice_private);
$alice_pub_details = openssl_pkey_get_details($alice);
$alice_public = $alice_pub_details["key"];
// Génération des clés ECC pour Bob
$bob = openssl_pkey_new($config);
openssl_pkey_export($bob, $bob_private);
$bob_pub_details = openssl_pkey_get_details($bob);
$bob_public = $bob_pub_details["key"];
// Calcul du secret partagé (ECDH)
$alice_resource = openssl_pkey_get_private($alice_private);
$bob_resource = openssl_pkey_get_private($bob_private);
$alice_shared = openssl_pkey_derive($bob_resource, $alice_resource, 32);
$bob_shared = openssl_pkey_derive($alice_resource, $bob_resource, 32);
if ($alice_shared === $bob_shared) {
echo "Clé secrète commune : " . bin2hex($alice_shared);
} else {
echo "Erreur dans l'échange de clés.";
}Explications
- Chaque partie génère sa paire de clés ECC.
openssl_pkey_derive()permet de dériver la clé secrète commune.- Cette clé (un simple flux binaire) peut ensuite servir à chiffrer les échanges avec AES, ChaCha20 ou tout autre algorithme symétrique.
Ce protocole ECDH est utilisé partout : dans TLS, SSH, Signal, WhatsApp ou encore Bitcoin.
ECC et la sécurité des communications web (HTTPS)
Lorsque vous naviguez sur un site sécurisé (avec HTTPS), votre navigateur et le serveur échangent une clé temporaire pour établir un canal chiffré. Depuis plusieurs années, la majorité des certificats SSL/TLS utilisent des courbes elliptiques pour cette étape, notamment grâce à ECDHE (Elliptic Curve Diffie-Hellman Ephemeral), une version éphémère d’ECDH.
Cela signifie que :
- Une nouvelle clé est générée pour chaque session,
- Même si une clé privée est compromise plus tard, les anciennes communications restent protégées (propriété appelée Perfect Forward Secrecy).
Ainsi, la cryptographie à courbe elliptique (ECC) est désormais une norme dans la sécurité des sites web, remplaçant progressivement RSA dans de nombreux serveurs modernes.
Les courbes les plus utilisées en cryptographie
Toutes les courbes elliptiques ne se valent pas. Certaines sont devenues des standards, d’autres sont recommandées pour leurs propriétés mathématiques.
Voici quelques-unes des plus courantes :
- prime256v1 (aussi appelée secp256r1) : la plus répandue, utilisée dans la majorité des certificats SSL.
- secp384r1 et secp521r1 : plus longues, donc plus sécurisées.
- Curve25519 : très populaire dans les protocoles modernes (Signal, WireGuard, OpenSSH), car elle est rapide et sûre.
En PHP, vous pouvez spécifier la courbe à utiliser via le paramètre "curve_name".
Par exemple :
$config = [
"private_key_type" => OPENSSL_KEYTYPE_EC,
"curve_name" => "secp384r1"
];Comparaison ECC vs RSA : que choisir ?
Prenons un instant pour comparer concrètement ces deux grands piliers de la cryptographie :
| Critère | RSA | ECC |
|---|---|---|
| Longueur de clé | 2048 à 4096 bits | 256 à 521 bits |
| Sécurité équivalente | 2048 bits RSA ≈ 256 bits ECC | Meilleure efficacité |
| Vitesse de génération | Lente | Rapide |
| Signature / vérification | Plus lourde | Plus rapide |
| Utilisation actuelle | Héritée (certificats, e-mails) | Majoritaire (TLS, mobiles, IoT) |
La conclusion est claire : ECC offre plus de sécurité pour moins de calculs, ce qui la rend incontournable dans les systèmes modernes, notamment dans les environnements contraints comme les objets connectés.
Vers l’avenir : ECC et cryptographie post-quantique
Malgré sa puissance, la cryptographie à courbe elliptique n’est pas invulnérable. L’arrivée future des ordinateurs quantiques remettra en question la sécurité de nombreux algorithmes asymétriques, y compris l’ECC et le RSA.
Pourquoi ?
Parce qu’un ordinateur quantique suffisamment puissant pourrait résoudre le problème du logarithme discret elliptique bien plus rapidement qu’un ordinateur classique, rendant les clés ECC vulnérables.
Cependant, cela ne signifie pas la fin de l’ECC. De nombreux chercheurs travaillent déjà sur des algorithmes post-quantiques, capables de résister à ce type de menace, tout en s’inspirant des concepts mathématiques de l’ECC.
Les courbes elliptiques pourraient ainsi évoluer vers de nouvelles formes de sécurité hybrides, combinant efficacité, compacité et résistance quantique.
Pourquoi comprendre l’ECC est essentiel
La cryptographie à courbe elliptique (ECC) est bien plus qu’un sujet de niche réservé aux experts en sécurité. C’est aujourd’hui une technologie fondamentale de l’Internet moderne. Chaque fois que vous vous connectez à un site sécurisé, que vous signez un document électronique, ou que vous échangez un message chiffré sur votre téléphone, il y a de grandes chances qu’une courbe elliptique protège vos données.
Comprendre les principes de base de l’ECC, c’est comprendre comment la confiance circule sur le web. Et en tant que développeur PHP, savoir manipuler des clés ECC, signer des messages ou établir un échange sécurisé, c’est acquérir une compétence concrète, utile et valorisante.
Car si les mathématiques sont le cœur de la cryptographie, la compréhension en est l’âme. Et désormais, vous savez comment les courbes elliptiques dessinent la sécurité numérique du monde d’aujourd’hui.

