Maths & développement web : Arbre de décision et probabilité

Si vous débutez en mathématiques appliquées ou en développement web, il arrive souvent un moment où les probabilités deviennent un casse-tête. On se retrouve devant des calculs qui s’accumulent, des évènements qui s’enchaînent, et l’impression qu’il manque toujours un petit quelque chose pour véritablement comprendre ce qui se passe. C’est précisément là qu’interviennent l’arbre de décision. Ces schémas simples et progressifs transforment des situations complexes en un chemin clair à suivre. Il permet d’explorer plusieurs scénarios à la fois, comme on le ferait dans un jeu vidéo en testant différents choix possibles avant de s’engager.

• Comprendre intuitivement les probabilités grâce à une méthode visuelle qui clarifie les situations complexes.
• Savoir analyser n’importe quel scénario incertain en construisant des arbres de décision fiables et faciles à lire.
• Pouvoir anticiper, optimiser et prendre de meilleures décisions dans le développement web comme dans la vie quotidienne.

Dans ce chapitre, nous allons prendre le temps d’apprendre à construire un arbre de décision, à le lire, à le manipuler et surtout à l’utiliser pour calculer n’importe quelle probabilité de manière intuitive. L’objectif est que vous puissiez, après cette lecture, tracer un arbre aussi naturellement que vous codez une fonction PHP ou une boucle en JavaScript. Ne vous inquiétez pas si vous avez l’impression de « ne pas être doué en maths », l’approche visuelle et progressive des arbres change vraiment la donne.

Nous allons prendre des exemples du quotidien, mais aussi des situations qui vous parleront si vous êtes développeur. Je suis convaincu que plus un concept se relie à des situations familières, plus il s’installe durablement. Alors installez-vous confortablement : vous allez découvrir un outil puissant qui rend les probabilités enfin accessibles, logiques et même… agréables.

Comprendre ce qu’est un arbre de décision

Un arbre de décision est un schéma qui permet de représenter plusieurs choix ou évènements qui se suivent. On parle d’« arbre » parce qu’il démarre toujours d’un point de départ unique, puis se divise en branches qui représentent les différents chemins possibles. Chaque branche correspond à un évènement, et chacune porte une probabilité associée.

Pour commencer, imaginez un carrefour. Vous arrivez en vélo, et vous pouvez aller soit à gauche, soit à droite. L’arbre fait la même chose : il visualise ces options, mais en ajoutant une information essentielle, la probabilité que chacune se produise.

L’avantage principal de cette approche, c’est qu’elle vous oblige à décomposer une situation complexe en petites étapes logiques. Les probabilités ne sont alors plus une formule abstraite, mais un ensemble de choix qui se suivent naturellement.

Dans un arbre de décision, on retrouve toujours les mêmes éléments : un point d’origine, des branches représentant les actions ou évènements possibles, et au bout, les résultats finaux. Chaque segment porte une probabilité, ce qui permet ensuite de calculer la probabilité de chaque chemin complet.

Vous pouvez vous représenter l’arbre comme une sorte de fil d’histoire. Il vous raconte ce qui peut arriver, étape après étape. Et comme toutes les bonnes histoires, il a plusieurs fins possibles.

Pourquoi utiliser un arbre de décision en probabilités ?

Les arbres de décision sont un outil presque magique pour comprendre les probabilités conditionnelles et les calculs en plusieurs étapes. Lorsque deux ou trois évènements s’enchaînent, il devient difficile de garder tous les cas possibles en tête. L’arbre permet de tous les visualiser d’un coup.

La principale raison d’utiliser un arbre de décision, c’est qu’il évite les erreurs. Il empêche de mélanger les situations, et surtout il vous force à considérer tous les cas. Beaucoup de gens, même des développeurs très logiques, font l’erreur de ne pas analyser tous les scénarios possibles et d’en oublier un. L’arbre, lui, ne laisse rien au hasard.

Un second avantage est qu’il s’adapte à n’importe quel niveau de complexité. Vous pouvez l’utiliser pour une situation toute simple, comme tirer une boule dans une urne, ou pour un problème plus avancé, comme simuler un comportement utilisateur sur une plateforme web. Plus la situation est complexe, plus l’arbre devient incontournable.

Enfin, l’arbre est un excellent support pédagogique. Si vous êtes formateur, blogueur, ou simplement quelqu’un qui aime comprendre ce qu’il fait, un arbre de décision permet de visualiser la logique qui se cache derrière un calcul. Même ceux qui ont « peur des maths » se retrouvent rassurés lorsqu’ils voient la situation représentée étape par étape.

Construire un arbre de décision : la méthode étape par étape

Commençons par construire un premier arbre très simple, histoire de poser les bases.

Imaginez que vous avez une boîte avec deux boules : une rouge et une bleue. Si vous tirez une boule au hasard, vous avez une chance sur deux d’obtenir la rouge, et une chance sur deux d’obtenir la bleue.

Pour représenter cela avec un arbre, vous tracez un point de départ, puis deux branches : l’une pour la boule rouge, l’autre pour la bleue. Chaque branche porte une probabilité : 1/2 pour la rouge, 1/2 pour la bleue.

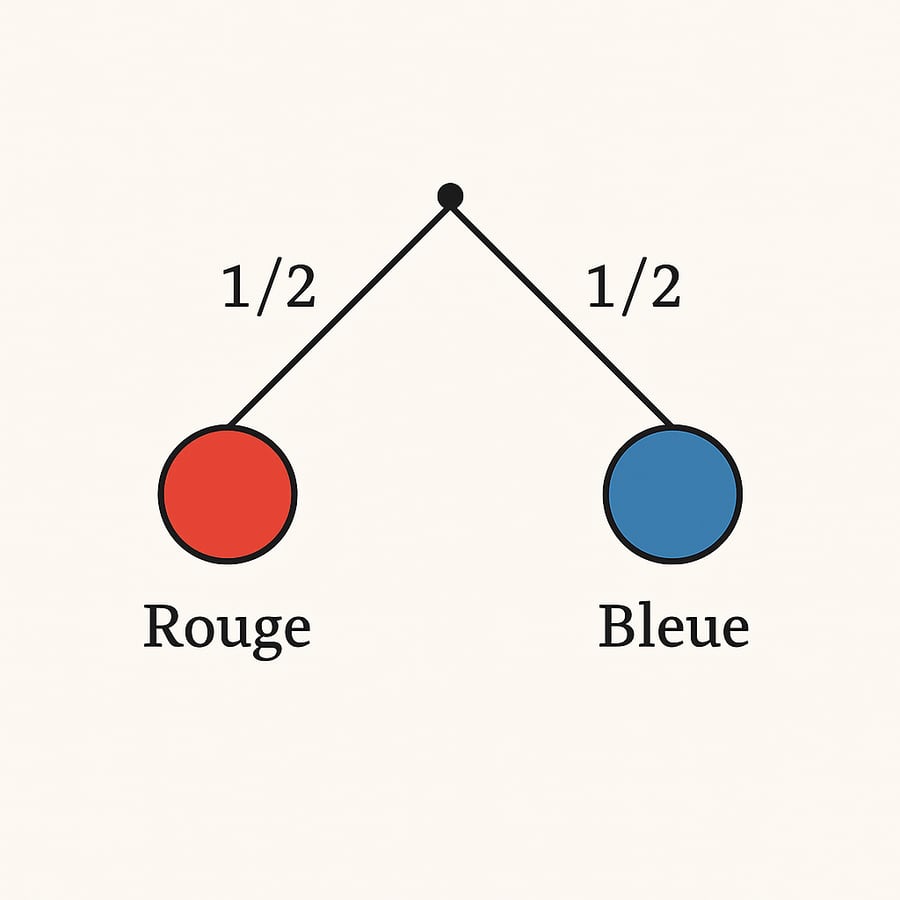
Cela semble trivial, mais ce schéma va servir de base pour toutes les situations plus complexes. L’idée est que chaque fois que vous avez un choix ou un évènement incertain, vous créez une branche.

Maintenant, imaginez que vous tirez une deuxième boule après la première, mais en la remettant dans la boîte. Cela signifie que le contenu revient toujours à deux boules identiques, et que les probabilités ne changent pas.

Votre arbre va alors se diviser en deux niveaux : le premier tirage, puis le deuxième. Le premier niveau a deux branches, le second niveau aussi. Au bout, vous obtenez quatre chemins possibles : rouge puis rouge, rouge puis bleue, bleue puis rouge, bleue puis bleue.

À chaque fois que vous descendez une branche, vous multipliez les probabilités. Par exemple, la probabilité de tirer rouge puis rouge est 1/2 × 1/2 = 1/4. C’est l’un des principes essentiels que nous allons utiliser tout au long du tutoriel.

Exemple concret : choisir un mot de passe sécurisé

Prenons un exemple plus moderne et plus en lien avec le développement web. Supposons qu’un utilisateur de votre site essaie de choisir un mot de passe. Vous avez analysé les statistiques et vous savez que 60 % des utilisateurs commencent leur mot de passe par une lettre, et 40 % par un chiffre.

Ensuite, vous remarquez que parmi ceux qui commencent par une lettre, 50 % ajoutent ensuite un chiffre. Et parmi ceux qui commencent par un chiffre, 80 % ajoutent une lettre.

Pour visualiser cela, un arbre est parfait. Il vous permet de voir d’un coup d’œil les quatre scénarios possibles.

Le premier niveau représente le premier caractère du mot de passe : lettre ou chiffre. Le second niveau représente le second caractère : lettre ou chiffre.

En utilisant l’arbre, vous pouvez facilement calculer la probabilité qu’un mot de passe commence par une lettre et soit suivi d’un chiffre. Il suffit de multiplier 0,6 par 0,5. Cela donne 0,3, donc 30 %.

Sans l’arbre, ce calcul peut sembler abstrait. Avec l’arbre, il devient visuel, logique, évident. Nous pouvons également le visualiser sous forme de tableau :

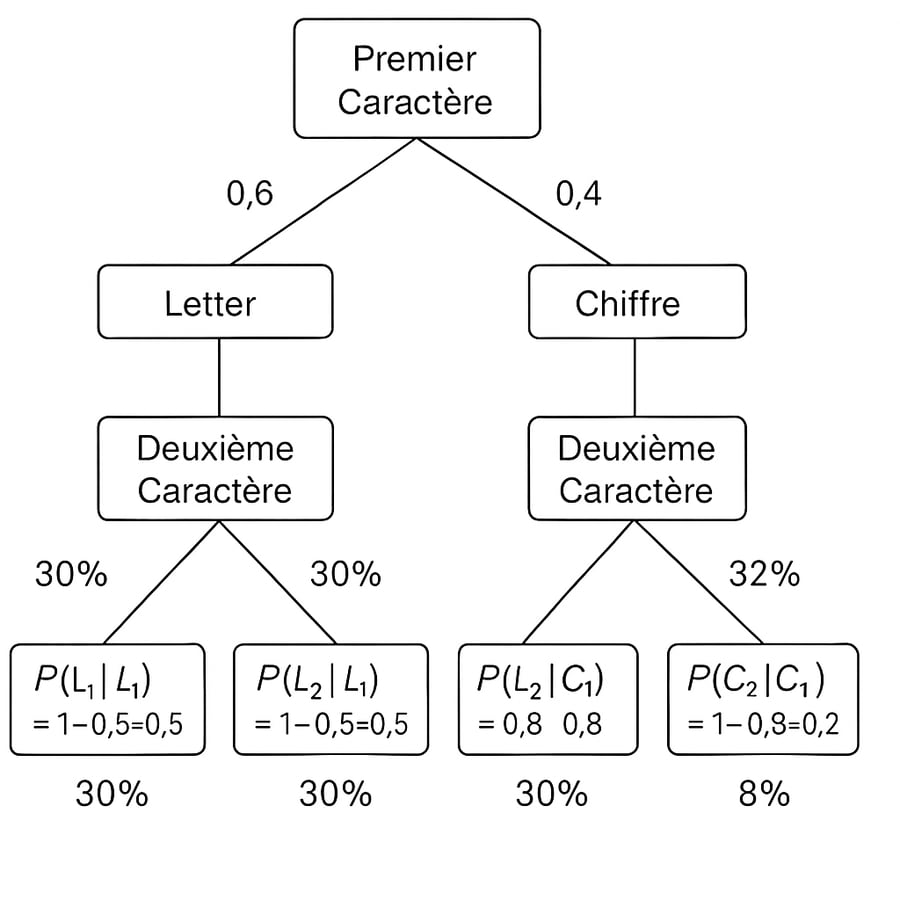
Comment lire un arbre de décision sans se tromper

Lire un arbre est aussi important que savoir le construire. Beaucoup de débutants tracent correctement leurs branches, mais se trompent dans leur interprétation.

Le premier conseil, c’est de suivre les branches dans le bon ordre. Un arbre se lit de gauche à droite ou de haut en bas, du point de départ vers les résultats finals. Chaque branche représente un choix ou un évènement.

Ensuite, vous devez toujours garder en tête que chaque niveau représente un évènement indépendant ou conditionné selon la situation. Si les probabilités changent en fonction de ce qui s’est passé avant, vous devez l’indiquer dans les branches du niveau suivant.

Le troisième conseil est de ne pas oublier la multiplication. Chaque fois que vous descendez une branche, vous multipliez la probabilité du segment précédent par celle du segment que vous empruntez. C’est cette multiplication qui donne la probabilité finale du chemin complet.

Enfin, un dernier conseil : vérifiez toujours que la somme des probabilités du premier niveau fait bien 1. Si vous avez deux branches au début, leurs probabilités doivent totaliser 100 %. Sinon, votre arbre est déjà faux dès le départ.

Probabilités conditionnelles : l’arbre comme solution visuelle

Une partie essentielle de tout travail sur les probabilités concerne les situations où le résultat d’un évènement dépend de ce qui s’est produit juste avant. Ce sont les probabilités conditionnelles. Beaucoup de débutants se sentent perdus à ce stade, car on a l’impression qu’il faut jongler entre plusieurs chiffres en même temps. Avec un arbre de décision, les probabilités conditionnelles deviennent pourtant des évidences.

Commençons par un exemple très connu : un sac contenant des cartes. Imaginons que vous ayez trois cartes blanches et une carte noire. Vous tirez une première carte sans la remettre, puis une deuxième. Le fait de ne pas remettre la première carte modifie la probabilité du second tirage. Si vous suivez la situation mentalement, vous allez vite vous mélanger. En revanche, avec un arbre, il suffit d’ajouter deux branches pour le premier tirage, puis de multiplier les branches du second en fonction du contenu restant.

Si vous tirez une carte blanche en premier, il reste deux blanches et une noire. Si vous tirez la noire en premier, il reste trois blanches. Vous voyez immédiatement que les probabilités du deuxième tirage sont différentes selon le chemin suivi. C’est exactement ce que l’on appelle une probabilité conditionnelle.

En observant l’arbre, vous comprenez instantanément que le second tirage n’a pas les mêmes chances selon la situation précédente. Ce qui semblait flou devient limpide, car chaque branche raconte clairement l’histoire complète. L’arbre transforme ce qui était abstrait en quelque chose de visuel, presque narratif.

On peut même aller plus loin. Si vous devez calculer la probabilité d’obtenir deux cartes blanches consécutives, il vous suffit de suivre la branche « blanche → blanche », puis de multiplier les probabilités du chemin. Vous n’avez jamais besoin d’inventer une formule compliquée, tout est sous vos yeux.

Les arbres pondérés : quand les chemins ne se valent pas

Tous les évènements ne se produisent pas avec la même fréquence. Dans le monde réel, certaines actions sont plus probables que d’autres. Les arbres pondérés permettent de représenter ces différences de manière très simple.

Prenons une anecdote courante dans le monde du web. Imaginez que vous observez le comportement des visiteurs de votre site. Vous remarquez que :

• 70 % quittent le site après la première page
• 20 % consultent une deuxième page
• 10 % se rendent sur votre formulaire de contact

Cette répartition est typique, et on la retrouve dans beaucoup de projets web débutants. Pour comprendre ce qui se passe, il est très utile de créer un arbre pondéré. Le premier niveau représente la première action du visiteur. Le second niveau, ce qu’il fait ensuite.

Si un visiteur regarde une deuxième page, vous constatez que 40 % d’entre eux s’inscrivent à votre newsletter, tandis que les autres continuent leur visite. Là encore, il serait difficile de tout visualiser dans votre tête. Avec un arbre, en revanche, vous obtenez une vue parfaite des différentes trajectoires possibles.

Les arbres pondérés sont également très utiles en marketing, en data science, et dans tous les domaines où l’on analyse des comportements humains. Ils permettent de comprendre rapidement où se trouvent les pertes, où se trouvent les opportunités, et où un simple ajustement pourrait faire toute la différence.

Le plus intéressant, c’est que vous pouvez même transformer cet arbre en stratégie d’optimisation : par exemple, si vous remarquez que peu de visiteurs atteignent votre formulaire de contact, mais que ceux qui y arrivent sont prêts à passer commande, l’arbre vous révèle immédiatement où renforcer votre site.

Exemple complet : analyser la fiabilité d’un test

Pour approfondir votre compréhension, étudions un exemple plus complexe, mais fondamental dans le domaine des probabilités : la fiabilité d’un test médical. Rassurez-vous, nous restons dans des chiffres simples et surtout dans une logique très pédagogique.

Supposons qu’un test détecte une maladie avec une précision de 95 %. Cela signifie que si une personne malade le passe, il a 95 % de chances d’être positif. Cependant, le test a aussi un taux de faux positifs de 2 %. Cela signifie que parmi les personnes non malades, 2 % auront malgré tout un résultat positif.

Enfin, imaginons que seulement 1 % de la population est réellement malade.

À ce stade, la plupart des gens se trompent. Ils pensent que si une personne obtient un test positif, elle a 95 % de chances d’être malade. Mais la réalité est beaucoup plus subtile. C’est précisément ce que les arbres de décision permettent de comprendre.

Commençons par un premier niveau : malade ou non malade. Cela correspond à 1 % contre 99 %.

Des formations informatique pour tous !

Débutant ou curieux ? Apprenez le développement web, le référencement, le webmarketing, la bureautique, à maîtriser vos appareils Apple et bien plus encore…

Formateur indépendant, professionnel du web depuis 2006, je vous accompagne pas à pas et en cours particulier, que vous soyez débutant ou que vous souhaitiez progresser. En visio, à votre rythme, et toujours avec pédagogie.

Découvrez mes formations Qui suis-je ?

Ensuite, pour chaque branche, nous ajoutons un deuxième niveau : test positif ou test négatif. Pour les malades, le test est positif 95 % du temps. Pour les non malades, il est positif 2 % du temps.

Lorsque vous tracez l’arbre au complet, vous voyez apparaître quatre scénarios :

• malade → test positif
• malade → test négatif
• non malade → test positif
• non malade → test négatif

Pour obtenir la probabilité réelle qu’une personne ayant obtenu un test positif soit réellement malade, il suffit de comparer les probabilités des chemins « test positif » entre eux. Et là, surprise : la très grande majorité des tests positifs proviennent en réalité de personnes non malades. Pourquoi ? Parce que même si le test est très fiable, la maladie est extrêmement rare.

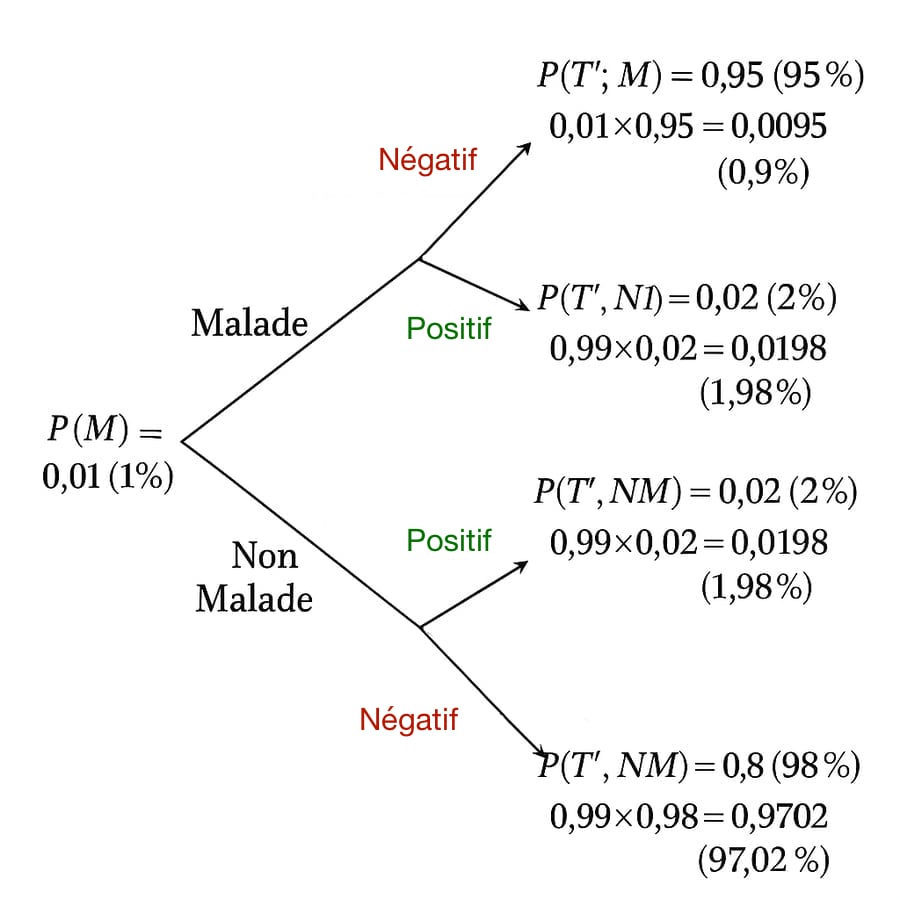
Cet exemple illustre parfaitement la puissance de l’arbre de décision pour comprendre des situations dans lesquelles nos intuitions nous trompent. Il met en lumière les chemins possibles, et surtout les proportions relatives entre eux. C’est un outil presque indispensable dès qu’une situation contient plusieurs niveaux d’incertitude.

Construire des arbres de décision dynamiques dans un cadre informatique

Si vous faites du développement web, vous avez sans doute déjà été confronté à des situations où il faut analyser des comportements d’utilisateurs, des flux de données ou des parcours différents selon différents choix. Les arbres de décision sont particulièrement utiles dans ces cas.

Les frameworks modernes, qu’il s’agisse de React, Vue ou même d’outils PHP orientés MVC (CodeIgniter), utilisent souvent des structures logiques inspirées des arbres. Quand vous codez un routeur, par exemple, vous créez mentalement des embranchements : si l’URL est ceci, alors afficher cette page ; sinon, passer à un autre contrôle.

Les arbres de décision fonctionnent sur la même idée, mais avec un objectif statistique. Imaginons que vous analysiez le parcours d’un utilisateur sur un site e-commerce. Après avoir vu la page d’accueil, il peut cliquer sur un produit, quitter le site ou faire une recherche interne. Chacun de ces choix a une probabilité mesurée par vos outils analytics.

Si vous ajoutez ensuite un deuxième niveau, comme « ajoute au panier », « lit les avis », ou « consulte un produit similaire », vous obtenez un arbre à plusieurs niveaux qui représenterait les parcours typiques. Ce schéma vous permet non seulement de comprendre le comportement réel des utilisateurs, mais aussi de prédire leur comportement futur.

Cette approche est très utilisée en machine learning. Dans les algorithmes de classification, les arbres de décision servent à déterminer automatiquement les chemins les plus efficaces pour prédire un résultat. Bien sûr, dans ce chapitre, nous restons dans une logique mathématique simple, mais il est intéressant de voir que la même structure conceptuelle existe dans des domaines très avancés.

Étude de cas : un arbre pour optimiser un formulaire de contact

Imaginons que vous possédiez un site sur lequel un utilisateur peut vous contacter via un formulaire. Vous remarquez que :

• 80 % des visiteurs voient le bouton « contact »
• 50 % cliquent dessus
• 20 % commencent à remplir le formulaire
• 10 % vont jusqu’au bout et valident l’envoi

Ces chiffres peuvent paraître décevants, mais ils sont très courants dans le web. Pour comprendre ce qui se passe, il suffit de tracer un arbre de décision reprenant chaque étape.

Le premier niveau représente les visiteurs qui voient le bouton. Le second niveau, ceux qui cliquent dessus. Le troisième, ceux qui commencent à écrire un message. Le quatrième, ceux qui valident le formulaire.

Une fois l’arbre construit, vous pouvez suivre chaque chemin et identifier où se situent les pertes. Dans notre exemple, la perte principale survient entre le clic sur le bouton et le début de la rédaction. Cela vous donne une piste très concrète d’amélioration : peut-être que la page de contact est trop longue à s’afficher, trop peu claire, trop intimidante ou encore trop chargée.

Cet arbre n’est pas simplement un outil statistique, c’est un révélateur. Il vous montre précisément où agir pour transformer davantage de visiteurs en contacts réels. Et lorsqu’on gère un site de manière professionnelle, ce type de structure visuelle fait gagner un temps précieux.

Les erreurs les plus fréquentes avec les arbres de décision

Même si les arbres de décision simplifient énormément la compréhension des probabilités, certaines erreurs reviennent régulièrement chez les débutants. Les connaître dès maintenant vous permettra non seulement d’éviter des pièges classiques, mais aussi de corriger rapidement vos raisonnements si vous sentez que quelque chose cloche.

La première erreur est d’oublier de vérifier que la somme des probabilités du premier niveau fait bien 1. Cela peut sembler anodin, mais c’est pourtant l’un des pièges les plus courants. Si vous commencez un arbre avec des probabilités incorrectes, tout ce que vous calculerez ensuite sera faux. C’est un peu comme coder un script PHP qui commence par une erreur de syntaxe : vous pouvez écrire un roman derrière, le fichier ne fonctionnera jamais.

La deuxième erreur fréquente consiste à confondre les probabilités conditionnelles et les probabilités indépendantes. Si un évènement dépend du précédent, les probabilités doivent être ajustées. Pourtant, beaucoup de gens laissent les mêmes pourcentages sur toutes les branches par habitude. L’arbre est justement là pour rappeler que la situation peut changer à chaque niveau, et que ces changements doivent être représentés.

Une troisième erreur est de multiplier les mauvaises valeurs. Certains suivent visuellement la bonne branche, mais se trompent dans les chiffres faute d’avoir pris le temps de noter clairement chaque probabilité sur son segment. Il est donc conseillé d’écrire systématiquement les probabilités sur les branches, même si elles paraissent évidentes. Cela évite des oublis et permet de relire l’arbre sans devoir tout recommencer.

Il existe aussi une erreur plus subtile, souvent observée chez les personnes qui manipulent les chiffres rapidement : ne pas tenir compte de tous les chemins. Par exemple, lorsqu’on cherche la probabilité d’un évènement final, certains ne considèrent qu’un seul scénario possible, alors qu’il en existe plusieurs conduisant au même résultat. L’arbre permet justement de visualiser ces possibilités, mais encore faut-il prendre le temps d’analyser toutes les branches concernées.

Enfin, on retrouve un dernier piège : tracer un arbre trop rapidement, sans prendre en compte l’ordre réel des évènements. L’arbre doit toujours respecter la chronologie. Si l’on inverse deux niveaux, les calculs deviennent incohérents, car les probabilités ne correspondent plus à la réalité chronologique.

L’apprentissage des arbres de décision demande un peu de rigueur au début, mais cette rigueur finit par devenir naturelle. Comme dans le développement web, les premières heures peuvent paraître exigeantes, mais une fois que la logique est intégrée, vous vous surprenez à appliquer ces raisonnements automatiquement.

Construire des arbres complexes : méthode progressive

Lorsque vous serez à l’aise avec les arbres simples, vous pourrez commencer à aborder des situations plus complexes. La tentation pourrait être de vouloir tout tracer d’un coup, mais il est bien plus efficace d’avancer étape par étape. La méthode suivante est très utilisée, même par les analystes professionnels.

La première étape consiste à écrire la liste des évènements dans l’ordre chronologique. Avant même de tracer un arbre, notez simplement ce qui va se passer : un évènement A, puis un évènement B, puis éventuellement un évènement C. Les probabilités ne viennent qu’après. Cette liste est la base structurelle de l’arbre.

Ensuite, vous pouvez commencer à tracer la première division. Chaque branche correspond à une option possible pour le premier évènement. N’ajoutez rien d’autre pour l’instant, contentez-vous d’obtenir un premier niveau clair et propre.

La troisième étape consiste à ajouter le deuxième niveau pour chaque branche du premier. Ce moment est important parce qu’il permet d’introduire les probabilités conditionnelles. Vous pouvez alors écrire les pourcentages ou fractions, et vous assurer qu’ils totalisent bien 100 % pour chaque embranchement.

Lorsque vous avez deux niveaux bien construits, vous pouvez passer au troisième, puis au quatrième, et ainsi de suite. L’erreur serait de commencer à tracer des branches multiples en essayant de gagner du temps. Comme dans un travail de développement web, le mieux est d’avancer bloc par bloc pour garder une structure maîtrisée.

Une fois toutes les branches tracées, vous pourrez alors vous occuper des calculs. Commencez par suivre un chemin complet et multipliez les probabilités une par une. Ensuite, passez au chemin suivant. À mesure que vous répétez l’exercice, vous verrez que cela devient très fluide.

Les arbres complexes peuvent paraître intimidants, mais ils ne sont finalement qu’une succession de petites étapes logiques. C’est exactement cette progression qui fait la force de la méthode : elle rend accessibles des situations qui, autrement, seraient presque impossibles à suivre mentalement.

Exemple avancé : un arbre de décision pour un jeu de société

Pour rendre la théorie plus vivante, examinons un exemple très concret tiré d’un jeu de société. Imaginons un jeu où un joueur doit piocher des cartes pour avancer d’une, deux ou trois cases. Les cartes sont réparties ainsi :

• 50 % des cartes permettent d’avancer d’une case
• 30 % permettent d’avancer de deux cases
• 20 % permettent d’avancer de trois cases

Après avoir avancé, le joueur lance un dé pour déterminer s’il peut rejouer. Sur un résultat pair, il rejoue. Sur un résultat impair, il passe son tour.

Pour comprendre toutes les trajectoires possibles en un seul « tour », un arbre de décision est particulièrement adapté.

Le premier niveau représente la carte tirée : une, deux ou trois cases. Le second niveau représente le résultat du dé. Le troisième niveau représente éventuellement un second tirage de carte si le joueur a obtenu un nombre pair.

Vous voyez rapidement que toutes les options ne mènent pas à la même distance totale parcourue. Par exemple, la probabilité d’avancer exactement trois cases en un tour dépend non seulement du type de carte tirée, mais aussi du fait de rejouer ou non. L’arbre met en lumière tous les chemins menant à un résultat donné.

Cet exemple illustre pourquoi les arbres de décision sont très utilisés dans le game design, mais aussi en intelligence artificielle, où l’on cherche à simuler des comportements complexes. L’arbre devient alors un outil de planification, presque comme un moteur de recherche parmi des milliers de possibilités.

Arbres de décision et développement web : prévoir les scénarios utilisateurs

Revenons au développement web, car les arbres ont une place très utile dans ce domaine. Lorsque vous concevez une interface utilisateur, vous devez souvent prévoir plusieurs scénarios possibles. Par exemple, imaginons un système d’inscription sur un site. Plusieurs choses peuvent se produire :

• L’utilisateur réussit l’inscription du premier coup.
• Il commet une erreur dans son email.
• Il oublie son mot de passe.
• Il abandonne le processus en cours de route.

Si vous souhaitez optimiser votre système, vous avez tout intérêt à tracer ces possibilités. Cela vous permet de visualiser quelles étapes posent le plus de problèmes. Si vous réalisez que 40 % des abandons surviennent au moment du choix du mot de passe, vous savez immédiatement sur quoi vous concentrer.

Dans un contexte professionnel, cet arbre peut devenir un véritable outil d’analyse. Il aide à identifier les points faibles d’un parcours utilisateur et à prioriser les améliorations. Les services marketing, UX, ou data l’utilisent très souvent, car il permet de comprendre les comportements réels et non pas supposés.

Calculer des probabilités finales : additionner les bons chemins

Maintenant que vous connaissez la méthode pour tracer un arbre complet et calculer la probabilité d’un chemin unique, il est temps de passer à l’étape suivante : calculer la probabilité totale d’un évènement donné.

Cette étape demande souvent d’additionner plusieurs chemins, car un même résultat peut être obtenu de différentes manières. Par exemple, imaginons une situation où vous cherchez la probabilité d’obtenir un total de quatre points dans un jeu où vous faites deux actions successives. Vous pouvez y arriver de plusieurs façons : une carte de deux points suivie d’une autre de deux points, une carte de trois points suivie d’une carte d’un point, etc.

Avec un arbre, vous visualisez facilement tous les chemins menant au même résultat final. Il vous suffit ensuite de calculer chaque chemin séparément (en multipliant les probabilités de chaque branche), puis d’additionner les résultats pour obtenir la probabilité globale.

Ce principe est essentiel : pour une même situation finale, il existe souvent plusieurs chemins possibles. L’arbre est justement là pour vous permettre de les repérer d’un seul coup d’œil. Il vous évite d’en oublier, ce qui est indispensable pour avoir un calcul correct.

Les arbres de décision ont cette capacité rare de transformer une situation qui semble confuse en une suite d’étapes parfaitement lisibles. Ils obligent à ralentir, à poser les éléments les uns après les autres, et surtout à se donner le temps de comprendre ce qui se joue réellement derrière un calcul de probabilité. Lorsque vous débutez, vous pouvez avoir l’impression que tout cela est trop abstrait, trop lointain, presque réservé à celles et ceux qui « sont bons en maths ». Pourtant, dès que l’on se met à tracer ces fameuses branches, quelque chose se débloque. Les évènements s’ordonnent, les chiffres prennent du sens, et la logique reprend naturellement le dessus.

L’un des plus beaux effets de cette méthode, c’est qu’elle offre de la clarté là où règne la confusion. Dans le développement web, dans la vie quotidienne, ou même dans un simple jeu de société, les arbres de décision vous permettent de prévoir, d’anticiper, et même parfois de repérer des évidences que l’on ne voyait pas à première vue. Ils deviennent un compagnon discret mais terriblement efficace dans votre manière de raisonner.

Il donne envie de comprendre, il apaise les appréhensions, et il montre que les probabilités ne sont pas ce mur de chiffres intimidant que l’on imagine souvent. Ce sont des histoires, des choix, des chemins qui se dessinent et que l’on suit pas à pas.

Alors, prenez le temps de tracer votre prochain arbre. Laissez-vous surprendre par sa simplicité. Et, qui sait, peut-être découvrirez-vous que les probabilités, finalement, ne sont pas qu’une question de chiffres, mais une façon de voir le monde d’un œil plus patient, plus logique… et parfois même plus amusant.

Alban

Fondateur de l’agence Créa-troyes.
Intervenant en Freelance.
Contactez-moi

crea-troyes.fr