Maths et développement web : Test statistique et A/B testing

Un domaine joue un rôle discret mais essentiel dans l’évolution d’un site ou d’une application : les mathématiques. Plus précisément, les mathématiques appliquées à la prise de décisions basées sur des données réelles : Test statistique et A/B testing.

À mesure qu’un site web accueille des visiteurs, ces visiteurs agissent, naviguent, cliquent, achètent ou quittent la page. Chacune de ces interactions est une information précieuse. Et c’est là que les tests statistiques entrent en scène. Ils permettent de déterminer si une amélioration sur votre site est réellement bénéfique ou si elle n’est qu’un coup de chance.

L’A/B testing, est une méthode qui compare deux versions d’une même page, d’un bouton ou d’un formulaire pour choisir la meilleure. Ce n’est pas seulement une idée marketing. C’est une application directe de la statistique, via des concepts tels que l’échantillonnage, l’hypothèse nulle, le taux de conversion ou la significativité.

• Comprendre comment prendre des décisions web basées sur des données fiables plutôt que sur l’intuition.
• Savoir comparer deux versions d’une page ou d’un élément pour choisir celle qui améliore réellement les conversions.
• Acquérir les bases nécessaires pour valider l’efficacité d’un modèle ou d’un changement avant de le déployer.

Ce chapitre vous guidera pas à pas, même si vous n’aimez pas les maths ou que vous n’avez pas touché à une équation depuis le lycée. L’objectif est de vous montrer que les statistiques ne sont pas réservées aux chercheurs ou aux calculatrices graphiques, mais qu’elles constituent un outil concret pour améliorer un site web, une boutique en ligne ou une application.

Pourquoi les mathématiques comptent dans le développement web

Lorsque l’on développe un site, on prend constamment des décisions : choisir la couleur d’un bouton, l’emplacement d’un formulaire, la longueur d’un texte, le prix d’un produit, etc. Très souvent, ces choix se font à l’instinct. On se dit qu’un bouton rouge attire plus l’œil, ou que mettre le formulaire plus haut augmentera les inscriptions.

Mais comment en être sûr ? Comment savoir si la nouvelle version d’une page est réellement meilleure ?

Parfois, le cerveau humain nous joue des tours. On croit qu’une version fonctionne mieux parce qu’elle “semble” mieux fonctionner, alors qu’en réalité, la différence n’est pas significative ou même totalement due au hasard. Le hasard est un acteur puissant. Donnez une pièce parfaitement équilibrée à quelqu’un qui la lance dix fois. Il est possible d’obtenir huit fois pile et deux fois face. Pourtant la pièce n’est pas truquée.

C’est la même chose pour vos données : Une amélioration apparente peut n’être qu’une fluctuation accidentelle. Le rôle des mathématiques ici est de vérifier si ce que l’on voit dans les chiffres est réel ou coïncident.

Avant tout : comprendre ce qu’est une donnée

Dans le contexte du web, une donnée peut être par exemple :

• un clic sur un bouton
• une durée passée sur une page
• un panier validé ou abandonné
• une inscription à une newsletter

Chaque utilisateur génère des données au fur et à mesure qu’il navigue.

Imaginons une page d’inscription simple. Sur 100 personnes qui la visitent, 5 s’inscrivent. On dit alors que le taux de conversion est de 5 %.

Ce taux devient un indicateur. Il permet de mesurer l’efficacité de la page. Si vous modifiez quelque chose (par exemple le texte du bouton), et que le taux passe à 7 %, il semble que la nouvelle version soit meilleure. Mais peut-on affirmer cela sans doute ?
Pas encore. Il faut tester.

A/B testing : la logique générale

L’A/B testing consiste justement à afficher deux versions d’un élément à deux groupes d’utilisateurs. Par exemple :

• Version A : bouton bleu “S’inscrire”
• Version B : bouton vert “Rejoindre maintenant”

Vous laissez les deux versions tourner pendant un certain temps. Puis vous comparez les taux de conversion. L’idée paraît simple, mais ce qui fait toute la différence, c’est de pouvoir affirmer :

“La version B est meilleure que la version A.”

Cela semble évident : il suffit de comparer les pourcentages. Mais la réalité est plus subtile. Si la version A convertit 5 % et la version B 7 %, vous devez vérifier si cette différence est statistiquement significative. Cela signifie :

• Est-ce que cette différence est due au changement ?
• Est-ce que, si on recommençait l’expérience, la différence pourrait disparaître ?

C’est exactement ici que les tests statistiques interviennent.

Imaginez un restaurant qui teste deux recettes de tarte aux pommes. Un soir, les clients goûtent la recette A, le lendemain la recette B. Par hasard, le soir de la recette B, il fait beau et les terrasses sont pleines. Plus de clients, plus de compliments. Le chef pourrait penser que la recette B est meilleure… alors qu’en réalité, la différence vient du contexte, pas de la recette.

C’est pour éviter ce genre de conclusions précipitées que l’on utilise des méthodes rigoureuses de comparaison.

Hypothèse nulle : le cœur des tests statistiques

Dans les tests statistiques, il existe un concept fondamental : l’hypothèse nulle (souvent notée H0).

L’hypothèse nulle dit : « Il n’y a pas de différence réelle entre la version A et la version B. » Vous partez du principe que vos modifications n’ont aucun effet. Ce n’est que lorsque les résultats montrent une différence suffisamment grande que l’on peut rejeter l’hypothèse nulle et conclure :

« La version B a réellement un meilleur impact que la version A. »

Ce mécanisme peut sembler contre-intuitif au début. On pourrait croire qu’on “cherche à prouver que le changement marche”. En réalité, on cherche à démontrer que l’effet n’est pas juste dû au hasard. Cette approche évite les illusions, les biais et l’enthousiasme trop rapide.

Le seuil de significativité

Lorsque l’on réalise un test statistique, on choisit un seuil appelé alpha, souvent égal à 0,05. Cela signifie :

« J’accepte seulement 5 % de chances de me tromper en affirmant qu’une différence existe. »

Si les résultats montrent une probabilité inférieure à ce seuil que la différence soit due au hasard, alors on peut affirmer que la nouvelle version est réellement meilleure. Ce seuil n’est pas parfait, mais il permet un compromis entre confiance et efficacité.

Exemple concret appliqué au web

Supposons que :

• Version A : 1000 visiteurs → 50 inscriptions → taux = 5 %
• Version B : 1000 visiteurs → 65 inscriptions → taux = 6,5 %

À première vue, la version B semble meilleure. Mais est-ce statistiquement significatif ?

Un test statistique (comme le test du Chi-deux ou le test de proportion) permet de répondre à la question : la différence observée est-elle suffisamment forte pour ne pas être due au hasard ?

Si oui, on adopte la version B. Si non, on garde la version A ou on continue de tester. Ce type de raisonnement est utilisé par les plateformes de géants du web (Amazon, Google, Facebook, Netflix) des milliers de fois par jour.

Test du Chi-deux

Le test du Chi-deux est un outil statistique qui permet de comparer des résultats observés avec des résultats qui auraient pu arriver simplement par hasard. Dans le contexte du web, on l’utilise par exemple pour comparer deux taux de conversion entre deux versions d’une page. L’idée est de regarder si la différence entre les deux versions est assez grande pour dire qu’elle ne vient pas seulement de la chance.

Si le test du Chi-deux indique que la différence est trop faible, alors on considère qu’il n’y a pas de preuve solide que l’une des versions soit meilleure que l’autre. Autrement dit, ce test permet de vérifier si une amélioration est réellement due à votre changement, et non à une simple fluctuation naturelle des données.

Test de proportion

Le test de proportion, lui, s’applique plus spécifiquement aux taux, comme un pourcentage de clics ou d’inscriptions. Imaginons que la version A convertit 5 % des visiteurs et la version B 7 %. Le test de proportion va calculer si cette différence est « suffisamment grande » pour être considérée comme significative. Si oui, vous pouvez dire que la version B améliore réellement la performance. Si non, cela signifie que même si les chiffres semblent différents, ils ne sont pas assez éloignés pour exclure le hasard. C’est donc un test très pratique et directement lié aux situations que l’on rencontre dans l’A/B testing.

Ces deux tests sont importants parce qu’ils apportent une rigueur dans la prise de décision. Sans eux, on pourrait faire de nombreux changements sur un site en croyant l’améliorer, alors qu’en réalité, on ne ferait qu’ajouter du bruit, voire dégrader l’expérience utilisateur. Avec eux, on avance avec preuve, méthode et confiance.

Comprendre la p-value sans formule

Le terme p-value fait souvent peur. Pourtant, il n’est pas si difficile à comprendre lorsqu’on le relie à une situation concrète. La p-value mesure la probabilité que les résultats observés soient dus au hasard, et non à votre modification.

Reprenons notre exemple du bouton :

• Version A : 5 % de conversions
• Version B : 6,5 % de conversions

Vous avez envie de dire que B est meilleure. La p-value vient vérifier si cette différence aurait pu se produire juste par chance, même si en réalité, A et B convertissent de la même manière. On peut la voir comme une question :

« Si la modification n’avait eu aucun effet, quelle est la probabilité que je puisse obtenir une différence aussi grande juste en tombant sur un échantillon plus favorable ? »

Si cette probabilité est très faible, alors cela renforce l’idée que votre modification a eu un impact réel.

Lorsque la p-value est inférieure à 0,05 (soit 5 %), on considère généralement que le résultat est statistiquement significatif. Cela signifie que l’on peut raisonnablement affirmer que la différence n’est pas seulement due au hasard.

Dit autrement : Plus la p-value est petite, plus vous pouvez être confiant dans votre changement.

Calculer la p-value revient donc à mesurer à quel point les résultats que vous observez auraient pu se produire si, en réalité, il n’y avait aucune différence entre vos deux versions. C’est comme si l’on demandait : « Si A et B étaient identiques, aurait-on quand même pu obtenir par hasard une différence aussi grande que celle que l’on voit ? ».

Pour répondre à cette question, on utilise soit une formule mathématique, soit un logiciel (ce qui est le plus courant). Le logiciel va comparer les données observées avec ce qui serait attendu si le hasard était le seul responsable. Plus la différence observée est “improbable” à expliquer par le hasard, plus la p-value est faible.

Il n’existe pas une seule formule de p-value, car elle dépend du type de test statistique utilisé. Cependant, dans le cadre de l’A/B testing, on utilise très souvent le test de proportion, qui donne une formule assez standard.

Voici la formule la plus courante pour comparer deux taux de conversion :

Des formations informatique pour tous !

Débutant ou curieux ? Apprenez le développement web, le référencement, le webmarketing, la bureautique, à maîtriser vos appareils Apple et bien plus encore…

Formateur indépendant, professionnel du web depuis 2006, je vous accompagne pas à pas et en cours particulier, que vous soyez débutant ou que vous souhaitiez progresser. En visio, à votre rythme, et toujours avec pédagogie.

Découvrez mes formations Qui suis-je ?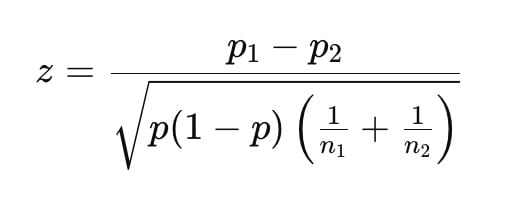

Puis la p-value est obtenue à partir du score z grâce à une table statistique (ou automatiquement via un logiciel).

• p1​ : taux de conversion de la version A
• p2 : taux de conversion de la version B
• n1 : nombre de visiteurs ayant vu la version A
• n2​ : nombre de visiteurs ayant vu la version B
• p : taux de conversion “moyen” des deux versions combinées

p = nombre total de conversions / nombre total de visiteurs

Une fois le score z calculé, on regarde où il se situe sur une courbe statistique appelée courbe normale. Plus ce z est “loin” de zéro, plus la différence entre A et B est considérée comme réelle et non due au hasard.

La p-value correspond alors à la probabilité que cette différence soit due à la chance. Un logiciel ou une bibliothèque (comme Excel, Python, R, ou même des sites web gratuits) calcule cela automatiquement.

Pour allez plus loin, découvrez notre Tutoriel complet sur R et RStudio.

Dans la pratique, la p-value est donc un score de doute. Une p-value élevée signifie que vos résultats peuvent très bien s’expliquer par le hasard, donc vous ne pouvez pas conclure. Une p-value basse (généralement inférieure à 0,05) signifie que la probabilité que la différence soit due au hasard est très faible. On considère alors que l’effet est réel.

L’important n’est pas de calculer la p-value soi-même (des outils le font très bien), mais de comprendre sa signification : elle vous dit si vous avez assez de preuves pour affirmer qu’un changement est réellement bénéfique.

L’intervalle de confiance : ce que les données “n’osent pas dire clairement”

Un autre outil essentiel est l’intervalle de confiance. Il sert à exprimer une fourchette dans laquelle la valeur réelle du taux de conversion a le plus de chances de se trouver.

Même si vous observez un taux de conversion de 6,5 % sur votre échantillon, ce n’est pas une valeur absolue. Elle fluctue. Le vrai taux est peut-être 6 %, peut-être 7 %, peut-être même un peu moins ou un peu plus. L’intervalle de confiance vient dire quelque chose comme :

« Nous pensons que le taux réel se situe probablement entre 6,2 % et 6,9 %. »

Ce genre de fourchette vous permet de décider plus sereinement. Si l’intervalle de confiance de la version B est entièrement supérieur à celui de la version A, alors B est réellement meilleure. Cela évite encore une fois les conclusions hâtives.

Comment mener un test A/B en pratique

À présent, passons à la pratique. Vous n’avez pas besoin d’être statisticien, ni de savoir coder un moteur d’analyse pour commencer à faire des tests A/B.

Cependant, il faut respecter quelques principes simples.

Première étape : définir clairement l’objectif

Vous devez savoir ce que vous cherchez à améliorer. Cela paraît évident, mais beaucoup de tests échouent parce que l’objectif est vague.

Souhaitez-vous améliorer :

• Le nombre d’inscriptions
• Le temps passé sur une page
• Le nombre de produits ajoutés au panier
• Le taux de clics sur un bouton
• Le nombre de contacts par formulaire

Choisissez un seul objectif par test. C’est essentiel, sinon les résultats deviennent ambigus.

Deuxième étape : changer un seul élément à la fois

Si vous changez la couleur du bouton, le texte, la taille, et l’emplacement en même temps, vous ne saurez jamais ce qui a fait la différence.

Un test A/B doit isoler une seule variable. Comme en cuisine, si vous testez une nouvelle recette, vous ne changez pas tous les ingrédients en même temps.

Troisième étape : laisser le test tourner suffisamment longtemps

C’est probablement l’étape la plus difficile émotionnellement. On aime décider vite. On regarde les premiers résultats, on voit que ça semble mieux… et on arrête tout. Erreur très fréquente !

À court terme, les données sont chaotiques. Parfois, la version A commence plus forte, puis la version B la dépasse, ou inversement. Il faut laisser le temps aux résultats de se stabiliser. Souvent, on recommande de laisser tourner un test :

• Au minimum une semaine
• Et jusqu’à atteindre un nombre suffisant de visiteurs (souvent quelques milliers, selon la taille du site)

Plus le volume de visiteurs est faible, plus il faut de patience.

Quatrième étape : analyser avec méthode

Une analyse réussie repose sur :

• Le taux de conversion observé
• La p-value ou le niveau de confiance
• L’intervalle de confiance

Même si vous ne calculez rien “à la main”, vos outils peuvent vous les fournir automatiquement.

Quels outils utiliser pour faire un A/B test

Il existe plusieurs solutions adaptées à différents niveaux techniques.

1. Google Optimize (anciennement très utilisé, remplacé par des alternatives depuis l’arrêt du service).
2. Matomo (open source, très respectueux de la vie privée, parfait si vous hébergez vous-même vos données).
3. Outils intégrés dans les CMS comme WordPress avec des extensions.
4. Solutions maison en PHP ou JavaScript (plus techniques mais très flexibles).

Pour débuter, il est parfaitement possible d’utiliser un outil sans code. Par exemple, avec Matomo ou une extension WordPress, vous pouvez créer deux versions d’une même page et laisser le plugin faire la répartition et l’analyse.

Ce qui compte, ce n’est pas l’outil : C’est la rigueur du raisonnement.

Exemple concret d’A/B test sur un site d’inscription

Prenons un exemple que l’on pourrait retrouver sur notre site Créa-Toyes. On propose des cours en visioconférence. Vous avez une page d’inscription avec un bouton :

“Je m’inscris maintenant”

Vous décidez de tester si un texte plus personnalisé fonctionne mieux, comme :

“Rejoignez-nous en direct”

Vous créez donc :

• Version A : bouton “Je m’inscris maintenant”
• Version B : bouton “Rejoignez-nous en direct”

Pendant une semaine, chaque visiteur reçoit l’une ou l’autre version au hasard. À la fin de la semaine :

• Version A : 2000 visiteurs, 110 inscriptions → taux 5,5 %
• Version B : 1900 visiteurs, 145 inscriptions → taux 7,6 %

La version B semble meilleure. Vous vérifiez la p-value : elle est inférieure à 0,05. Vous examinez l’intervalle de confiance : les valeurs de B sont supérieures à celles de A.

Vous pouvez alors dire que la version B ne fonctionne pas mieux par hasard, mais qu’elle améliore réellement les inscriptions. Vous adoptez donc la version B.

Vous venez de prendre une décision basée sur des données, et non sur une impression.

Validation de modèles : aller plus loin que l’A/B testing

L’A/B testing vérifie l’efficacité d’une modification en comparant deux versions. Mais parfois, vous allez vouloir aller plus loin. Par exemple, si vous mettez en place un système de recommandation de produits, un moteur de recherche interne, ou un algorithme de tri personnalisé. Ces systèmes reposent souvent sur des modèles mathématiques.

Un modèle doit être validé avant d’être utilisé. La validation permet de vérifier qu’il se comporte bien sur des données qu’il n’a pas encore vues. On sépare donc les données en deux groupes :

• Données d’entraînement, pour construire le modèle
• Données de test, pour vérifier la fiabilité

Cette méthode évite la sur-adaptation, un phénomène où un modèle fonctionne très bien sur les données connues mais échoue dès qu’on lui présente des cas nouveaux.

Cela revient un peu à un élève qui apprend ses devoirs par cœur sans comprendre. Il a l’air brillant, mais dès qu’un exercice change légèrement, il ne sait plus quoi faire. Valider un modèle permet donc de s’assurer qu’il n’apprend pas simplement par répétition, mais qu’il comprend réellement les régularités derrière les données.

Lors de la création d’une application de recommandations de films, une équipe de développeur s’était rendu compte que leur modèle recommandait presque uniquement des films très connus. Leur système semblait efficace : les utilisateurs cliquaient souvent sur les recommandations.

En réalité, leur modèle ne recommandait pas les films parce qu’ils correspondaient aux goûts des utilisateurs, mais simplement parce qu’ils étaient populaires. La validation sur de nouvelles données a révélé cette erreur. Sans ce test, ils auraient pensé que leur modèle fonctionnait… alors qu’il ne faisait que reproduire une mode.La validation permet de démasquer ce genre d’illusion.

Les mathématiques, loin d’être une abstraction scolaire, s’avèrent être un outil concret et extrêmement puissant dans la prise de décision en développement web. Elles permettent de transformer une intuition en une démarche rigoureuse, de distinguer ce qui fonctionne réellement de ce qui semble fonctionner, et de construire des systèmes fiables qui évoluent avec les besoins des utilisateurs.

L’A/B testing n’est pas seulement une technique marketing. C’est une manière d’écouter votre audience, de respecter leur comportement réel, plutôt que de vous fier à un instinct ou à une mode. De la même manière, la validation de modèles garantit que l’intelligence que vous introduisez dans vos outils est solide, adaptable et réaliste.

En intégrant progressivement ces concepts, même à très petite échelle, vous gagnerez en confiance, en précision et en efficacité. Votre site ne sera plus seulement “bien conçu”. Il deviendra vivant, construit sur des observations tangibles et des décisions éclairées.

Et surtout, n’oubliez jamais que les mathématiques, dans ce contexte, ne sont pas une montagne. Elles sont un fil conducteur. Un fil qui ne demande pas à être maîtrisé d’un coup, mais simplement à être suivi avec patience.

Alban

Fondateur de l’agence Créa-troyes.
Intervenant en Freelance.
Contactez-moi

crea-troyes.fr