Régression linéaire simple, Machine learning : Prédire un prix

Le Machine learning, ou apprentissage automatique en français, est aujourd’hui au cœur de nombreuses applications qui façonnent notre quotidien. La régression linéaire également. Qu’il s’agisse de recommandations sur des plateformes de streaming, d’outils de reconnaissance vocale ou encore de systèmes de prédiction financière, il est partout. Mais lorsque l’on débute, il peut sembler difficile de comprendre par où commencer et comment mettre en pratique ces concepts dans des projets concrets.

La régression linéaire est l’un des modèles les plus simples et les plus accessibles pour se lancer dans le Machine learning. Derrière ce nom un peu technique se cache une idée intuitive : trouver une ligne droite qui explique au mieux la relation entre deux variables. Prenons un exemple concret que tout le monde peut comprendre : prédire le prix d’une maison en fonction de sa surface. Plus une maison est grande, plus son prix a tendance à augmenter. La régression linéaire simple permet de modéliser cette relation et de faire des prédictions fiables à partir de données réelles.

Dans ce tutoriel, nous allons non seulement expliquer ce qu’est la régression linéaire et à quoi elle sert, mais aussi comment l’implémenter de manière pratique avec du code en PHP, grâce à une bibliothèque de Machine learning.

À la fin de ce chapitre sur le Machine Learning en PHP, vous serez capable non seulement de comprendre la logique qui se cache derrière ce modèle, mais aussi de l’utiliser concrètement dans vos propres projets.

Qu’est-ce que la régression linéaire simple ?

La régression linéaire simple est une technique statistique qui consiste à expliquer une variable par une autre. On parle souvent de variable dépendante et de variable indépendante. La variable dépendante est celle que l’on veut prédire, et la variable indépendante est celle dont on pense qu’elle influence la première.

Dans notre exemple, la variable dépendante est le prix d’une maison, car c’est ce que l’on veut estimer. La variable indépendante est la surface en mètres carrés, car nous supposons que plus la surface est grande, plus le prix augmente.

Mathématiquement, la régression linéaire simple cherche à trouver une équation de la forme :

Prix = a × Surface + b

• « a » est la pente de la droite. Elle indique de combien le prix augmente lorsque la surface augmente d’une unité.
• « b » est l’ordonnée à l’origine, c’est-à-dire la valeur de base du prix lorsque la surface est égale à zéro (même si, dans la réalité, une maison de zéro mètre carré n’existe pas, ce paramètre est nécessaire pour le calcul).

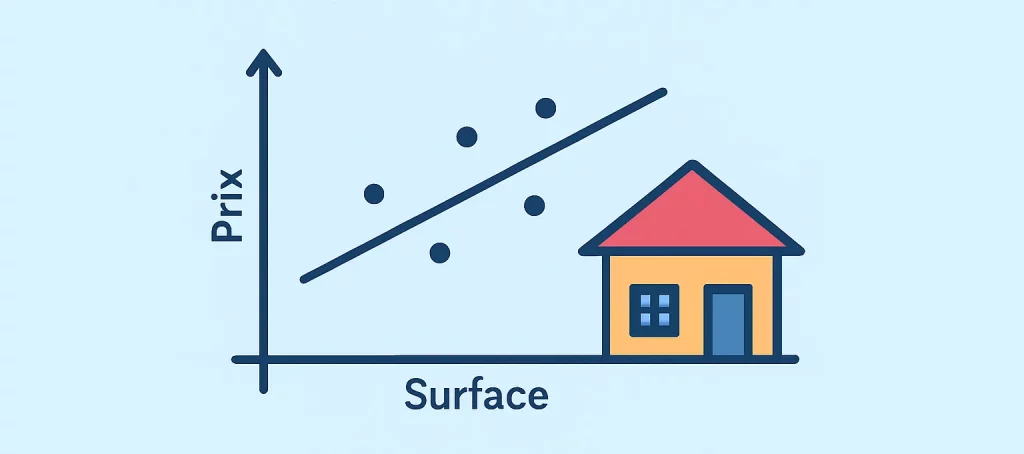
En clair, la régression linéaire cherche à ajuster une ligne droite qui passe au plus près des points représentant nos données (dans notre cas, différentes maisons avec leurs surfaces et leurs prix).

L’intérêt de cette approche est qu’elle est très intuitive. On peut même la visualiser facilement : si l’on trace les surfaces des maisons sur l’axe horizontal et les prix sur l’axe vertical, la régression linéaire correspond à une droite qui suit au mieux la tendance générale.

La régression linéaire et la fonction affine en mathématiques

Pour bien comprendre la régression linéaire, il est utile de faire un petit détour par les mathématiques et, en particulier, par la notion de fonction affine. Même si le Machine learning permet de manipuler les données sans forcément entrer dans les détails mathématiques, savoir ce qui se cache derrière l’algorithme vous aidera à mieux l’utiliser et à interpréter ses résultats.

Qu’est-ce qu’une fonction affine ?

Une fonction affine est une fonction mathématique de la forme :

f(x) = ax + b

• Le a représente la pente de la droite. Il indique la vitesse à laquelle la valeur de la fonction augmente (ou diminue, si a est négatif) lorsque la variable x augmente.
• Le b représente l’ordonnée à l’origine, c’est-à-dire le point où la droite coupe l’axe vertical (y) lorsque x = 0.

Graphiquement, une fonction affine est une droite. C’est exactement ce que cherche à construire la régression linéaire : une droite qui colle au mieux aux points de vos données.

La régression linéaire comme ajustement d’une fonction affine

Lorsque l’on applique la régression linéaire, on suppose que la relation entre notre variable explicative (dans notre exemple, la surface d’une maison) et notre variable dépendante (le prix de la maison) peut être représentée par une fonction affine.

Autrement dit, on suppose que le prix peut être écrit sous la forme :

Prix = a × Surface + b

Ici :

• a est le coefficient directeur qui traduit combien le prix augmente pour chaque mètre carré supplémentaire.
• b est la valeur de départ, correspondant au prix « théorique » d’une maison de surface nulle (même si ce cas n’a pas de sens dans la réalité, il reste nécessaire pour l’équation).

L’algorithme de régression linéaire consiste donc à trouver les valeurs optimales de a et de b pour que la droite passe au plus près possible de l’ensemble des points représentant nos données.

La méthode des moindres carrés

Pour trouver cette droite idéale, la régression linéaire utilise une méthode appelée méthode des moindres carrés.

Imaginons que nous ayons plusieurs points (chaque point représentant une maison avec sa surface et son prix). Si nous traçons une droite au hasard, certains points seront au-dessus de la droite, d’autres en dessous.

La méthode des moindres carrés consiste à mesurer la distance verticale entre chaque point et la droite (on appelle cela une erreur ou un résidu), puis à élever ces distances au carré pour éviter les valeurs négatives. Ensuite, l’algorithme cherche la droite qui minimise la somme de toutes ces erreurs au carré.

En d’autres termes, la meilleure droite de régression est celle qui colle le plus près possible à l’ensemble des données.

Exemple concret

Prenons un exemple très simple avec trois maisons :

• Maison 1 : 50 m², 100 000 €
• Maison 2 : 100 m², 200 000 €
• Maison 3 : 150 m², 300 000 €

Ici, on voit tout de suite que la relation est parfaitement linéaire : le prix double lorsque la surface double. La fonction affine qui modélise cette situation est :

Prix = 2000 × Surface

Dans ce cas précis, l’algorithme n’aurait aucune difficulté à trouver la pente a = 2000 et l’ordonnée b = 0.

Mais dans des données réelles, les points ne sont pas alignés aussi parfaitement. C’est là que la régression linéaire prend tout son sens : elle cherche la droite la plus proche possible, même si les points sont dispersés.

Pourquoi c’est important de comprendre ce lien ?

Savoir que la régression linéaire est en réalité une fonction affine ajustée sur vos données vous donne une vision claire du modèle. Cela vous permet de mieux interpréter les résultats.

Par exemple, si vous entraînez un modèle et qu’il vous donne l’équation :

Prix = 1800 × Surface + 20 000

Cela signifie que chaque mètre carré supplémentaire ajoute en moyenne 1800 € au prix, et qu’une maison de très petite surface aurait une valeur de départ d’environ 20 000 € (selon le modèle).

Vous pouvez alors décider si ce résultat est cohérent avec votre expérience ou vos connaissances du marché. Si ce n’est pas le cas, c’est peut-être que les données utilisées ne sont pas représentatives, ou que le modèle choisi n’est pas le plus adapté.

À quoi sert la régression linéaire simple ?

La régression linéaire simple est utilisée depuis longtemps en statistique, en économie, en science sociale et désormais en Machine learning. Elle sert principalement à deux choses : expliquer et prédire.

Premièrement, elle permet d’expliquer la relation entre deux variables. Par exemple, elle peut montrer à quel point la surface influence le prix d’une maison. Si la pente de la droite est forte, cela signifie que la surface a un impact important sur le prix. Si la pente est faible, cela signifie que la surface n’a qu’un rôle limité.

Deuxièmement, elle permet de prédire de nouvelles valeurs. Supposons que vous ayez un jeu de données comprenant des dizaines de maisons avec leur surface et leur prix. Grâce à la régression linéaire, vous pouvez estimer le prix d’une maison dont vous connaissez la surface, mais pas encore le prix. Cela peut être très utile dans l’immobilier, mais aussi dans d’autres domaines comme la prévision des ventes, la consommation énergétique ou encore l’évolution de la température en fonction du temps.

Enfin, la régression linéaire est un modèle très simple, ce qui la rend idéale pour l’apprentissage. Elle constitue une première étape avant de découvrir des modèles plus complexes, comme la régression multiple (plusieurs variables explicatives) ou les réseaux de neurones.

Ses avantages et ses limites

Comme toute méthode, la régression linéaire simple présente des forces mais aussi des faiblesses. Il est important de bien les connaître avant de l’utiliser.

Le premier avantage est sa simplicité. La régression linéaire est facile à comprendre, à visualiser et à mettre en place. Même sans bagage mathématique avancé, il est possible d’en saisir le fonctionnement et d’en tirer des résultats.

Le deuxième avantage est sa rapidité. Contrairement à des modèles de Machine learning plus complexes, elle demande peu de ressources et s’exécute rapidement, même sur des données volumineuses.

Un autre avantage est son interprétabilité. Contrairement à un réseau de neurones, par exemple, où l’on a du mal à expliquer pourquoi une prédiction a été faite, la régression linéaire offre une équation claire. On sait exactement comment chaque variable influence le résultat.

Les limites

En revanche, la régression linéaire simple a des limites importantes. La première est qu’elle ne fonctionne bien que si la relation entre les deux variables est linéaire. Si la relation est courbée ou plus complexe, la droite de régression ne sera pas adaptée et les prédictions risquent d’être très imprécises.

Ensuite, elle est sensible aux valeurs extrêmes. Par exemple, si dans vos données une maison a une surface anormalement grande ou petite, cela peut fortement influencer la droite de régression et fausser le modèle.

Enfin, elle est limitée à une seule variable explicative. Or, dans la réalité, le prix d’une maison dépend de nombreux facteurs : surface, localisation, nombre de chambres, état général, etc. La régression linéaire simple ne prend en compte qu’un seul de ces paramètres, ce qui peut donner une vision trop simpliste.

Des formations informatique pour tous !

Débutant ou curieux ? Apprenez le développement web, le référencement, le webmarketing, la bureautique, à maîtriser vos appareils Apple et bien plus encore…

Formateur indépendant, professionnel du web depuis 2006, je vous accompagne pas à pas et en cours particulier, que vous soyez débutant ou que vous souhaitiez progresser. En visio, à votre rythme, et toujours avec pédagogie.

Découvrez mes formations Qui suis-je ?

Quand utiliser la régression linéaire simple ?

La régression linéaire simple n’est pas un outil universel. Elle est très efficace dans certains cas, mais totalement inadaptée dans d’autres. Pour bien savoir quand l’utiliser, il faut garder à l’esprit trois grands principes.

Quand la relation est linéaire

La régression linéaire simple est idéale lorsque la relation entre deux variables est proportionnelle ou presque linéaire. Dans notre exemple immobilier, il est raisonnable de penser que plus une maison est grande, plus son prix augmente de manière régulière. Mais si l’on essayait de prédire la température d’un café en fonction du temps écoulé depuis qu’il a été servi, la courbe serait plutôt en forme de courbe exponentielle (chute rapide au début, puis stabilisation). Dans ce cas, la régression linéaire ne serait pas adaptée.

Quand une seule variable explicative suffit

Elle est à privilégier lorsque vous n’avez qu’une seule variable indépendante forte. Dans le cas d’une maison, la surface est un bon indicateur du prix, même si ce n’est pas le seul. Mais si vous souhaitez prendre en compte plusieurs critères (quartier, année de construction, nombre de chambres), il faudra passer à une régression multiple.

Quand on a besoin d’un modèle simple et rapide

Enfin, la régression linéaire simple est parfaite pour les situations où vous avez besoin d’un modèle facile à comprendre et à mettre en œuvre rapidement. Elle peut servir de première étape pour analyser des données avant d’explorer des modèles plus sophistiqués.

Utilisez la régression linéaire simple quand la relation entre vos données est linéaire, qu’une seule variable explicative est pertinente et que vous voulez un modèle simple, rapide et compréhensible.

Exemple pratique : Prédire le prix d’une maison en fonction de sa surface

Passons maintenant à la partie concrète : mettre en place une régression linéaire simple en PHP pour prédire le prix d’une maison en fonction de sa surface.

Le choix de la bibliothèque de Machine learning en PHP

Contrairement à Python, où l’on dispose de bibliothèques très connues comme scikit-learn, le Machine learning en PHP est moins répandu. Mais il existe tout de même des outils très intéressants. Nous allons utiliser ici la bibliothèque Rubix ML, qui est l’une des plus complètes pour le Machine learning en PHP.

Rubix ML est une librairie open-source qui propose de nombreux algorithmes, dont la régression linéaire. Elle est conçue pour être simple à utiliser, même si vous n’avez pas de grandes connaissances en mathématiques.

Installation de Rubix ML

Avant de coder, il faut installer la bibliothèque via Composer, le gestionnaire de dépendances de PHP. Si vous ne l’avez pas encore installé, vous pouvez télécharger Composer depuis son site officiel.

Une fois Composer disponible sur votre machine, ouvrez un terminal dans votre projet PHP et tapez :

composer require rubix/ml

Cela téléchargera et installera Rubix ML dans votre projet. Vous pourrez ensuite l’utiliser dans vos fichiers PHP grâce à l’autoload généré par Composer.

Préparer nos données

Imaginons que nous ayons un petit jeu de données représentant des maisons avec leur surface et leur prix. Dans un vrai projet, ces données viendraient probablement d’une base de données ou d’un fichier CSV. Pour simplifier, nous allons créer un tableau en PHP.

<?php

require 'vendor/autoload.php';

use Rubix\ML\Datasets\Labeled;
use Rubix\ML\Regressors\Ridge;
use Rubix\ML\Datasets\Unlabeled;

// Nos données : surfaces (m²) et prix (en milliers d’euros)
$surfaces = [50, 60, 80, 100, 120, 150, 200];
$prix = [100, 120, 160, 200, 240, 300, 400];

// Création du dataset
$dataset = Labeled::build(
    array_map(function ($s) {
        return [$s]; // chaque valeur doit être dans un tableau
    }, $surfaces),
    $prix
);

Ici, nous avons défini 7 maisons avec leur surface et leur prix. Chaque surface est mise dans un tableau car Rubix ML attend des données multidimensionnelles (même si nous n’avons qu’une seule variable).

Choisir et entraîner le modèle

Rubix ML propose plusieurs modèles de régression. Nous allons utiliser Ridge Regression, qui est une version améliorée de la régression linéaire classique et qui évite certains problèmes comme le surajustement.

// Création du modèle de régression
$estimator = new Ridge();

// Entraînement du modèle sur notre dataset
$estimator->train($dataset);

À ce stade, notre modèle a appris la relation entre la surface et le prix à partir des données fournies.

Faire une prédiction

Maintenant que notre modèle est entraîné, nous pouvons lui demander de prédire le prix d’une maison pour une surface donnée. Par exemple, combien coûterait une maison de 90 m² ?

// Prédire le prix pour une maison de 90 m²
$prediction = $estimator->predict([[90]]);

echo "Le prix estimé pour une maison de 90 m² est : " . $prediction . " milliers d’euros.";

Le modèle va calculer le prix estimé en utilisant la droite de régression qu’il a apprise. Le résultat sera affiché directement dans le terminal ou le navigateur, selon votre configuration.

Comprendre le code pas à pas

Prenons un moment pour décortiquer ce que nous venons de faire :

1. Nous avons préparé nos données sous forme de deux tableaux, l’un pour les surfaces et l’autre pour les prix.
2. Nous avons construit un dataset adapté à Rubix ML avec Labeled::build().
3. Nous avons choisi un modèle de régression (Ridge) et nous l’avons entraîné avec train().
4. Nous avons utilisé predict() pour obtenir une estimation sur une nouvelle donnée.

Chaque étape correspond à une logique claire : préparer les données, entraîner le modèle, puis utiliser le modèle pour prédire.

Comment enrichir et améliorer les données

La qualité d’un modèle de régression linéaire dépend en grande partie de la qualité et de la quantité des données utilisées pour l’entraîner. Si vos données sont trop pauvres, trop limitées ou mal préparées, même le meilleur algorithme ne pourra pas donner des résultats fiables. Voyons ensemble comment améliorer progressivement notre modèle.

Augmenter la quantité de données

Le premier moyen d’améliorer un modèle est de lui fournir davantage d’exemples. Dans notre cas, plus nous avons de maisons réelles avec leur surface et leur prix, plus la droite de régression sera proche de la tendance réelle du marché immobilier.

Si vous n’avez que quelques points (comme dans notre exemple avec seulement 7 maisons), le modèle risque d’être approximatif. Avec plusieurs centaines ou milliers d’exemples, la prédiction devient beaucoup plus robuste.

Nettoyer les données

Il est essentiel de s’assurer que les données sont fiables. Dans le cas de l’immobilier, il peut arriver que certains prix soient aberrants (par exemple, une maison très grande vendue à un prix extrêmement bas, ou inversement). Ces données dites outliers peuvent fausser la droite de régression, car l’algorithme essaiera de les intégrer dans le calcul.

Une bonne pratique est donc d’analyser les données en amont, et d’écarter celles qui ne semblent pas cohérentes.

Normaliser les données

Même si dans notre exemple nous n’avons qu’une seule variable (la surface), il est souvent conseillé de normaliser ou standardiser les données lorsqu’elles sont de grande amplitude. Cela signifie ramener les valeurs dans une échelle plus homogène, par exemple entre 0 et 1. Cela facilite l’apprentissage et rend les calculs plus stables.

Ajouter de nouvelles variables

La régression linéaire simple ne prend en compte qu’une seule variable explicative. Mais dans le monde réel, il est rare qu’un seul facteur suffise à expliquer un phénomène. Pour notre exemple, le prix d’une maison ne dépend pas seulement de sa surface.

On pourrait ajouter d’autres critères, comme :

• la localisation (ville, quartier),
• le nombre de chambres,
• l’année de construction,
• l’existence d’un jardin ou d’un garage,
• la proximité des commerces et écoles.

En intégrant ces nouvelles variables, on passe de la régression linéaire simple à la régression linéaire multiple (notre prochain chapitre). Le principe reste le même, mais au lieu d’une droite, on cherche à ajuster un plan ou un hyperplan qui prend en compte plusieurs dimensions. Cela permet d’obtenir des prédictions beaucoup plus proches de la réalité.

Diviser les données en deux ensembles

Une bonne pratique du Machine learning est de diviser les données en deux parties :

• un jeu d’entraînement, qui sert à apprendre le modèle,
• un jeu de test, qui sert à vérifier la précision des prédictions.

Sans cette étape, vous risquez d’obtenir un modèle qui semble très précis sur vos données actuelles mais qui échoue dès qu’il rencontre de nouvelles situations. On appelle cela le surapprentissage (ou overfitting).

Avec Rubix ML, il est facile de séparer un dataset en deux. Par exemple :

list($training, $testing) = $dataset->randomize()->split(0.8);

Ici, 80 % des données serviront à l’entraînement, et 20 % serviront à tester la précision du modèle.

Mesurer la performance du modèle

Enfin, il est important de mesurer si le modèle est bon ou non. Pour la régression linéaire, on utilise souvent des métriques comme l’erreur quadratique moyenne (MSE) ou le R² (coefficient de détermination).

Rubix ML propose des outils pour calculer ces mesures et évaluer objectivement la performance de votre modèle. Cela permet de comparer plusieurs versions de votre modèle et de garder la meilleure.

La régression linéaire simple est bien plus qu’un simple concept statistique. C’est une porte d’entrée vers le monde fascinant du Machine learning, car elle incarne l’équilibre entre simplicité et efficacité.

Dans ce chapitre, nous avons commencé par comprendre la logique de la régression linéaire, puis nous avons vu ses avantages, ses limites et les situations où elle est pertinente. Nous avons ensuite mis en pratique un exemple concret en PHP grâce à la bibliothèque Rubix ML, en construisant un modèle capable de prédire le prix d’une maison en fonction de sa surface. Enfin, nous avons exploré les façons d’améliorer ce modèle : enrichir les données, nettoyer les anomalies, ajouter des variables supplémentaires et mesurer les performances.

Ce qu’il faut retenir, c’est que la régression linéaire n’est pas seulement un outil académique. C’est un modèle réellement utile dans la vie courante, que ce soit pour l’immobilier, la prévision des ventes, l’analyse économique ou encore la modélisation scientifique. Elle constitue une base solide pour progresser vers des méthodes plus avancées, comme la régression multiple, les arbres de décision ou encore les réseaux de neurones.

Apprendre la régression linéaire, c’est apprendre à traduire une intuition en équation, à transformer des données brutes en informations utiles et exploitables. Et c’est aussi comprendre qu’en Machine learning, la clé du succès réside moins dans la complexité des algorithmes que dans la qualité des données et la pertinence des choix.

Si vous débutez dans ce domaine, n’hésitez pas à expérimenter. Testez différentes surfaces, enrichissez vos jeux de données avec de vraies annonces immobilières, comparez plusieurs modèles et mesurez leurs résultats. Chaque essai vous apportera une meilleure compréhension et une nouvelle compétence.

En résumé, la régression linéaire simple est un premier pas essentiel vers l’univers du Machine learning. Et comme souvent en programmation, le meilleur apprentissage vient en pratiquant. Alors lancez-vous : vos premiers modèles sont à portée de main, et chaque ligne de code vous rapproche un peu plus de la maîtrise de l’intelligence artificielle appliquée.

Mais attention, ne confondez pas Machine Learning et Intelligence artificielle !

Chapitre 3 : Régression linéaire multiple →

Alban

Fondateur de l’agence Créa-troyes.
Intervenant en Freelance.
Contactez-moi

crea-troyes.fr