Loi géométrique : comment l’utiliser en développement web

Vous êtes développeur web, étudiant, autodidacte ou simplement curieux, et vous tombez un jour sur ce terme un peu intimidant : la loi géométrique. Cette loi de probabilité est partout autour de nous, y compris dans le développement web. Il s’agit d’une une idée extrêmement simple : combien de tentatives faut-il avant qu’un événement réussisse pour la première fois ? Que ce soit un utilisateur qui clique enfin sur un bouton, un joueur qui gagne une partie, ou un script qui attend qu’une condition soit vraie, la loi géométrique permet de modéliser l’attente du succès.

• Comprendre quand et pourquoi la loi géométrique s’applique face aux situations d’attente, d’échec et de réussite répétée.
• Acquérir un outil de réflexion utile en développement web pour anticiper des comportements réels.
• Gagner en confiance face aux probabilités en découvrant qu’une loi mathématique peut être simple, concrète et exploitable.

Dans ce chapitre, nous allons partir de zéro, sans prérequis, pour comprendre la loi géométrique pas à pas, avec des mots simples, des exemples concrets et du code.

Qu’est-ce que la loi géométrique ?

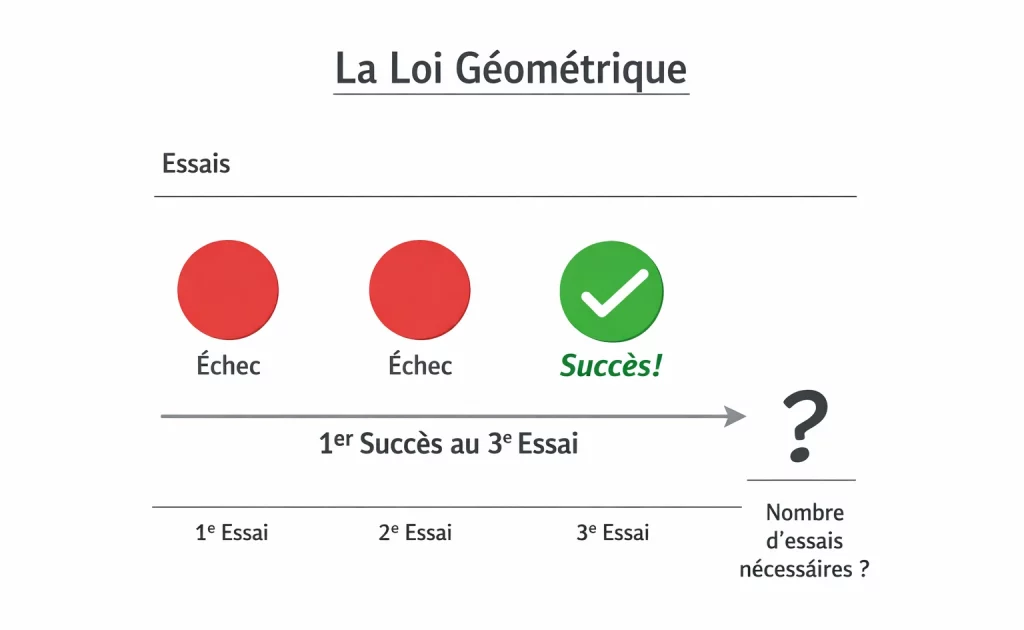
La loi géométrique est une loi de probabilité qui sert à répondre à une question très précise :

Combien d’essais sont nécessaires avant d’obtenir un premier succès ?

On ne cherche pas à savoir combien de succès il y aura, ni quand le deuxième arrivera. On s’intéresse uniquement au premier succès.

👉 Si vous débutez totalement : Initiations aux probabilités

Exemple immédiat

Imaginez une situation très simple :

• Vous lancez une pièce.
• Succès = obtenir pile.
• Échec = obtenir face.
• Vous recommencez jusqu’à tomber sur pile.

La loi géométrique permet de modéliser le nombre de lancers nécessaires avant le premier pile.

Cela peut être 1, 2, 5 ou 20 lancers… personne ne sait à l’avance. Mais la probabilité de chaque scénario peut être calculée.

Les conditions indispensables

La loi géométrique s’applique uniquement si quatre conditions sont respectées :

1. L’expérience est répétée plusieurs fois
2. Chaque essai est indépendant du précédent
3. Il n’y a que deux issues possibles : succès ou échec
4. La probabilité de succès est toujours la même

Si ces quatre règles sont réunies, alors vous êtes exactement dans le cadre de la loi géométrique.

Pourquoi cette loi est-elle si utile en développement web ?

À première vue, on pourrait penser que la loi géométrique ne concerne que les jeux de hasard. En réalité, elle modélise des comportements très humains, que l’on retrouve constamment sur le web.

Par exemple :

• Un utilisateur qui tente plusieurs fois avant de réussir une connexion
• Un visiteur qui rafraîchit une page jusqu’à voir une mise à jour
• Un joueur qui recommence une partie jusqu’à gagner
• Un script qui répète une action jusqu’à ce qu’une condition soit remplie

Dans tous ces cas, on répète une tentative jusqu’à ce que le succès arrive pour la première fois. Et c’est précisément le terrain de jeu de la loi géométrique.

La variable aléatoire expliquée simplement

En maths, on parle souvent de “variable aléatoire”. Dit comme ça, ça fait peur… alors qu’en réalité, c’est très simple.

Dans le cadre de la loi géométrique :

La variable aléatoire représente le nombre d’essais nécessaires avant le premier succès.

Par exemple :

• X = 1 → succès immédiat
• X = 3 → deux échecs puis un succès
• X = 10 → neuf échecs avant réussir

Rien de plus.

La formule de la loi géométrique expliquée simplement

Voici la fameuse formule :

$$P(X=k)=(1-p{)}^{k-1}\times p$$

Avant de fermer l’onglet 😄, prenons le temps de la traduire en français.

Que signifie chaque élément ?

• p : la probabilité de succès à chaque essai
• k : le numéro de l’essai où le succès arrive
• (1 − p) : la probabilité d’échec

La formule dit simplement ceci :

Pour réussir au kᵉ essai,
il faut échouer k − 1 fois, puis réussir une fois.

Exemple concret de la formule de la loi géométrique

Supposons que :

• la probabilité de succès est de 20 %
• donc p = 0,2
• la probabilité d’échec est 0,8

Quelle est la probabilité de réussir au 3ᵉ essai ?

• échec au 1er essai → 0,8
• échec au 2e essai → 0,8
• succès au 3e essai → 0,2

Calcul :$$0,8\times 0,8\times 0,2=0,128$$

👉 Il y a 12,8 % de chances de réussir exactement au troisième essai.

---

Un jour, en testant un formulaire d’inscription sur un site, je me suis rendu compte que certains utilisateurs tentaient plusieurs fois avant de réussir. Mot de passe trop court, erreur de confirmation, captcha raté… ils recommençaient, encore et encore, jusqu’à passer.

Sans le savoir, ils vivaient une loi géométrique en temps réel : chaque tentative avait la même probabilité de réussite, et le succès arrivait… quand il arrivait. Ces lois “théoriques” sont en fait très humaines.

Simuler la loi géométrique en JavaScript

Voyons maintenant comment simuler une loi géométrique en JavaScript, avec un exemple très simple.

Simulation d’un succès avec probabilité p

function tentative(p) {
  return Math.random() < p;
}

Cette fonction renvoie :

• true → succès
• false → échec

Compter le nombre d’essais avant succès

function loiGeometrique(p) {
  let essais = 0;

  while (true) {
    essais++;
    if (tentative(p)) {
      return essais;
    }
  }
}

console.log(loiGeometrique(0.2));

👉 Cette fonction renvoie le nombre d’essais nécessaires avant le premier succès.
Chaque appel donne un résultat différent, mais le comportement global suit la loi géométrique.

Les propriétés fondamentales de la loi géométrique

Maintenant que vous comprenez ce qu’est la loi géométrique et comment elle fonctionne, il est temps de s’arrêter sur ses propriétés essentielles. Ce sont elles qui font toute la puissance (et parfois les pièges) de cette loi de probabilité.

L’absence de mémoire : une idée contre-intuitive

C’est une propriété déroutante au premier abord. La loi géométrique possède une propriété très particulière appelée l’absence de mémoire.

Dit comme ça, on pourrait croire à une métaphore poétique. En réalité, c’est une notion mathématique très précise, et surtout contre-intuitive pour l’être humain.

L’absence de mémoire veut dire ceci :

Peu importe le nombre d’échecs déjà survenus,
la probabilité de succès au prochain essai reste exactement la même.

Autrement dit, le système ne se souvient de rien.

Supposons que :

• la probabilité de succès est de 10 %
• vous avez déjà échoué 20 fois

Intuitivement, on pourrait se dire :

Des formations informatique pour tous !

Débutant ou curieux ? Apprenez le développement web, le référencement, le webmarketing, la bureautique, à maîtriser vos appareils Apple et bien plus encore…

Formateur indépendant, professionnel du web depuis 2006, je vous accompagne pas à pas et en cours particulier, que vous soyez débutant ou que vous souhaitiez progresser. En visio, à votre rythme, et toujours avec pédagogie.

Découvrez mes formations Qui suis-je ?

“Statistiquement, ça devrait bientôt passer…”

Mais mathématiquement :

• la probabilité de réussir au prochain essai est toujours 10 %

Ni plus, ni moins.

Cette propriété est fondamentale, car elle permet d’éviter une erreur très fréquente : le biais du joueur.

C’est cette petite voix intérieure qui dit :

“J’ai tellement perdu que je vais forcément gagner maintenant.”

En loi géométrique, cette idée est fausse. Chaque essai est un nouveau départ, sans historique.

L’espérance : combien d’essais en moyenne ?

L’espérance d’une loi géométrique représente :

le nombre moyen d’essais nécessaires avant le premier succès

Ce n’est pas une prédiction exacte, mais une tendance moyenne observée sur un grand nombre de répétitions.

La formule de l’espérance est très simple :

$$E(X)=\frac{1}{p}$$Où :

• p est la probabilité de succès

Si la probabilité de succès est de :

• 50 % → espérance = 2 essais
• 20 % → espérance = 5 essais
• 5 % → espérance = 20 essais

👉 Plus le succès est rare, plus l’attente moyenne est longue.

Attention à l’interprétation : Dire que l’espérance est de 5 essais ne signifie pas que vous réussirez au 5ᵉ essai. Cela signifie que sur un grand nombre de tentatives, la moyenne se stabilise autour de cette valeur. C’est une nuance importante !

C’est exactement le même principe qu’une moyenne statistique.

Quand utiliser la loi géométrique ?

La loi géométrique est très efficace… à condition de l’utiliser au bon endroit.

Vous pouvez utiliser la loi géométrique si :

• vous répétez une action
• chaque tentative est indépendante
• le succès est binaire (oui / non)
• la probabilité reste constante
• vous cherchez le premier succès

C’est souvent le cas dans :

• les simulations
• les jeux
• les systèmes de retry
• l’analyse comportementale
• certains algorithmes

Les cas où elle ne s’applique pas

En revanche, la loi géométrique n’est pas adaptée si :

• la probabilité évolue avec le temps
• les essais dépendent les uns des autres
• vous cherchez plusieurs succès
• il y a plus de deux issues possibles

Dans ces situations, d’autres lois de probabilité sont plus pertinentes.

La loi géométrique appliquée au développement web

C’est ici que les choses deviennent vraiment intéressantes pour un développeur.

Exemple 1 : tentatives de connexion

Imaginons un utilisateur qui tente de se connecter à un site.

• Succès : identifiants corrects
• Échec : identifiants incorrects
• Chaque tentative a la même probabilité de réussite

👉 Le nombre de tentatives avant la première connexion réussie peut être modélisé par une loi géométrique.

Cela permet par exemple de :

• mesurer la difficulté perçue d’un formulaire
• anticiper le nombre moyen d’erreurs
• améliorer l’UX

Exemple 2 : clic sur un bouton

Sur une page web :

• chaque visiteur a 5 % de chances de cliquer sur un bouton
• il revient plusieurs fois sur le site

La loi géométrique permet d’estimer :

• le nombre moyen de visites avant le premier clic
• la patience nécessaire avant une conversion

Exemple 3 : système de retry côté serveur

Côté back-end, on rencontre souvent ce schéma :

• on tente une requête
• si elle échoue, on recommence
• on s’arrête dès que ça fonctionne

Ce comportement correspond exactement à une loi géométrique.

Exemple de simulation de la loi géométrique en PHP

Voici un exemple simple et pédagogique en PHP.

function tentative($p) {
    return mt_rand() / mt_getrandmax() < $p;
}

function loiGeometrique($p) {
    $essais = 0;

    while (true) {
        $essais++;
        if (tentative($p)) {
            return $essais;
        }
    }
}

echo loiGeometrique(0.2);

À chaque exécution :

• le nombre d’essais varie
• mais la distribution globale suit la loi géométrique

Simulation statistique pour mieux comprendre

Pour vraiment sentir la loi géométrique, rien de mieux qu’une simulation à grande échelle.

Exemple : moyenne observée

let total = 0;
let simulations = 100000;

for (let i = 0; i < simulations; i++) {
  total += loiGeometrique(0.2);
}

console.log(total / simulations);

👉 Vous observerez une moyenne très proche de 5, ce qui correspond bien à l’espérance théorique.

C’est souvent à ce moment-là que la loi géométrique “clique” vraiment.

Pourquoi cette loi est précieuse pour un développeur

La loi géométrique permet de :

• raisonner sur l’attente
• anticiper des comportements
• simuler des scénarios réalistes
• prendre de meilleures décisions techniques

Même si vous ne l’écrivez jamais noir sur blanc, elle structure beaucoup de raisonnements implicites.

---

La loi géométrique n’est pas une curiosité mathématique réservée aux manuels scolaires. C’est une façon élégante et puissante de modéliser l’attente, l’échec et le succès, des notions profondément humaines que l’on retrouve partout sur le web.

En tant que développeur, comprendre cette loi, c’est gagner un nouvel outil mental : celui qui permet de prendre du recul, de raisonner en probabilités et de mieux anticiper le comportement réel des utilisateurs ou des systèmes.

Et surtout, c’est une excellente porte d’entrée vers un monde passionnant où les maths ne sont plus abstraites, mais deviennent des alliées concrètes du développement web.

Si cet article vous a donné envie d’aller plus loin, c’est mission accomplie.