Loi de Fisher : comprendre les maths du web moderne

Les mathématiques et le développement web semblent parfois appartenir à deux mondes opposés. D’un côté, des formules abstraites, de l’autre, des lignes de HTML, de CSS ou de JavaScript destinées à créer des interfaces concrètes et interactives. Pourtant, ces deux univers sont bien plus liés qu’on ne l’imagine. La loi de Fisher fait partie de ces concepts mathématiques que l’on croise rarement de manière explicite dans le développement web, mais qui influencent énormément la façon dont les données sont analysées, comparées et interprétées. Comprendre ce principe, sans être mathématicien, permet de mieux raisonner sur la fiabilité des résultats, les performances ou encore les choix algorithmiques.

• Comprendre et interpréter correctement des chiffres et éviter les conclusions hâtives basées uniquement sur des moyennes trompeuses.
• Développer un raisonnement plus fiable pour comparer des performances, des comportements utilisateurs ou des résultats techniques dans des projets web.
• Gagner en maturité de développeur en adoptant une logique d’analyse des données plus rigoureuse, utile pour prendre de meilleures décisions produit et techniques.

Dans ce chapitre, vous allez découvrir la loi de Fisher en partant de zéro. Nous allons la décortiquer pas à pas, l’illustrer avec des exemples simples, puis voir comment elle s’applique concrètement dans des situations réelles de développement web, avec du code accessible aux débutants.

Qu’est-ce que la loi de Fisher ?

La loi de Fisher, que l’on appelle plus précisément le critère de Fisher, est un outil mathématique issu des statistiques. Elle a été introduite par Ronald Fisher, un statisticien britannique du XXᵉ siècle, avec une idée assez simple en apparence : mesurer à quel point deux groupes de données sont bien séparés.

Autrement dit, la loi de Fisher sert à répondre à une question très concrète :

Est-ce que deux ensembles de valeurs sont réellement différents, ou est-ce qu’ils se ressemblent trop pour tirer une conclusion fiable ?

Pour vulgariser, imaginez que vous compariez deux groupes d’utilisateurs sur un site web. Le premier groupe a vu une ancienne version d’une page, le second une nouvelle version. Vous constatez une différence de comportement, par exemple sur le taux de clic. La loi de Fisher permet d’évaluer si cette différence est réellement significative ou simplement due au hasard.

Derrière ce principe se cache une idée clé : comparer la distance entre les moyennes des groupes par rapport à leur dispersion interne. Plus les groupes sont éloignés les uns des autres et moins leurs valeurs sont dispersées, plus la séparation est nette. Nous allons découvrir cela en détail.

Une explication sans formules compliquées

Même si la loi de Fisher repose sur une formule mathématique, il est tout à fait possible de la comprendre sans entrer immédiatement dans les calculs.

Prenons un exemple simple. Vous mesurez le temps que mettent des visiteurs à remplir un formulaire. Sur une première version du formulaire, la moyenne est de 45 secondes. Sur une version optimisée, la moyenne descend à 35 secondes. À première vue, cela semble mieux. Mais si les temps sont très variables, allant de 5 secondes à 2 minutes dans les deux cas, la différence de moyenne peut être trompeuse.

La loi de Fisher ne se contente pas de regarder la moyenne. Elle tient compte de la stabilité des données. Si les valeurs sont très dispersées, la conclusion sera plus prudente. Si au contraire les données sont regroupées autour de la moyenne, la différence devient beaucoup plus crédible.

C’est exactement cette logique qui rend la loi de Fisher si utile dans l’analyse de données liées au web.

À quoi sert la loi de Fisher concrètement pour un développeur web ?

Dans un contexte plus général, la loi de Fisher est utilisée pour évaluer la pertinence d’une séparation entre des groupes. Elle est très présente dans des domaines comme la statistique, le machine learning ou l’analyse de performances.

En développement web, on la retrouve de manière indirecte dès que l’on cherche à comparer des comportements, des performances ou des résultats mesurés. Elle intervient par exemple dans l’analyse de tests A/B, dans l’évaluation d’algorithmes de recommandation ou encore dans le filtrage de données utilisateur.

Ce qui est important à retenir, c’est que la loi de Fisher n’est pas un outil réservé aux experts. Elle apporte une logique de raisonnement que tout développeur peut adopter : ne jamais se fier uniquement à une valeur moyenne, mais toujours tenir compte de la variabilité des données.

Quand utiliser la loi de Fisher ?

La loi de Fisher devient pertinente dès que vous êtes confronté à des comparaisons. Si vous avez deux versions d’un composant, deux stratégies d’affichage ou deux algorithmes produisant des résultats, elle permet de mieux comprendre lequel est réellement plus efficace.

Elle est particulièrement utile lorsque les différences sont subtiles. Si une nouvelle fonctionnalité améliore légèrement un indicateur, il est tentant de conclure trop vite. La loi de Fisher aide à prendre du recul et à éviter des décisions basées sur des impressions trompeuses.

Dans le développement web moderne, où tout est mesuré, comparé et optimisé, ce type de raisonnement devient un véritable atout.

Pour la petite histoire, lors d’un projet de refonte de formulaire, on avait constaté une baisse du taux d’abandon après une modification visuelle. Tout le monde s’est réjoui… jusqu’à ce qu’on se rende compte que les données provenaient d’une période très particulière, avec peu de trafic et des comportements atypiques. La moyenne avait baissé, mais la dispersion était énorme.

Vous comprendrez qu’un chiffre seul ne raconte jamais toute l’histoire. Sans le savoir, vous venez de toucher du doigt exactement ce que la loi de Fisher cherche à formaliser.

Les bases mathématiques, sans douleur

Mathématiquement, la loi de Fisher repose sur un rapport entre deux éléments : la différence entre les moyennes des groupes et la variance à l’intérieur de chaque groupe. Plus ce rapport est élevé, plus la séparation est considérée comme fiable.

Formule mathématique de la loi de Fisher

Pour deux groupes $G_1$G1​ et $G_2$G2​ :

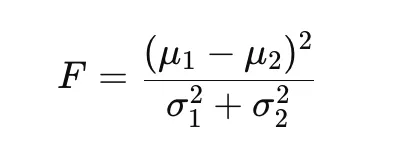
Signification de chaque terme

• ${\mu }_1$μ1​ : Moyenne du premier groupe de données.
• ${\mu }_2$μ2​ : Moyenne du second groupe de données.
• ${\sigma }_1^2$σ12​ : Variance du premier groupe (mesure de la dispersion autour de la moyenne).
• ${\sigma }_2^2$σ22​ : Variance du second groupe.

Pour aller plus loin : Variance et écart-type

Comment interpréter cette formule

Le numérateur (en haut de la fraction) mesure l’écart entre les moyennes des deux groupes. Le dénominateur (en bas de la fraction) mesure le bruit, c’est-à-dire la dispersion interne des données.

Plus le résultat $F$F est élevé, plus les deux groupes sont nettement séparés. Plus il est faible, plus les groupes se ressemblent ou se chevauchent.

Autrement dit, la loi de Fisher répond à cette question essentielle :

La différence observée est-elle grande par rapport à l’instabilité des données ?

Pourquoi cette formule est logique ?

Si deux groupes ont des moyennes très différentes mais des valeurs très dispersées, la séparation est incertaine. Si les moyennes sont différentes et les données très regroupées, la séparation est fiable.

La formule pénalise donc automatiquement les données instables, ce qui la rend très pertinente pour l’analyse réelle, notamment en développement web.

Vous n’avez pas besoin de mémoriser la formule pour l’instant. Ce qui compte, c’est l’intuition. Une bonne séparation, ce n’est pas seulement une différence visible, c’est une différence cohérente et stable.

Dans la prochaine partie, nous verrons comment traduire cette logique en situations concrètes de développement web, avec des exemples simples en JavaScript et des données que vous pourriez réellement rencontrer dans vos projets.

Comprendre la logique de Fisher avec un exemple simple

Avant même d’écrire la moindre ligne de code, il est essentiel de bien comprendre le raisonnement derrière la loi de Fisher. En développement web, ce raisonnement est souvent plus important que la formule elle-même.

Imaginons un cas très courant. Vous gérez un site et vous cherchez à améliorer le taux de clic sur un bouton d’inscription. Vous testez deux versions : un bouton bleu et un bouton vert. Pendant plusieurs jours, vous mesurez le nombre de clics obtenus chaque jour pour chaque version.

À la fin du test, vous constatez que le bouton vert a une moyenne légèrement supérieure. Le réflexe naturel serait de conclure que le bouton vert fonctionne mieux. Pourtant, ce raisonnement est incomplet. Pourquoi ? Parce qu’une moyenne ne suffit jamais à raconter toute l’histoire.

La loi de Fisher vous invite à poser une question plus fine :

La différence observée est-elle suffisamment nette par rapport à la variabilité des résultats ?

Si les résultats fluctuent énormément d’un jour à l’autre, la différence peut être purement accidentelle. En revanche, si les résultats sont stables et bien distincts, la conclusion devient beaucoup plus fiable.

La loi de Fisher appliquée à un test A/B

Le test A/B est probablement l’exemple le plus parlant pour comprendre l’intérêt de la loi de Fisher dans le développement web. Même si vous n’avez jamais utilisé ce terme, vous avez sûrement déjà appliqué ce principe sans le savoir.

Un test A/B consiste à proposer deux versions d’un même élément à des utilisateurs différents, puis à comparer leurs comportements. Cela peut concerner une page, un formulaire, un bouton ou même un simple texte.

La loi de Fisher intervient ici comme un outil d’analyse. Elle permet de mesurer la qualité de la séparation entre les deux groupes d’utilisateurs. Si les performances de chaque version sont trop proches ou trop instables, il est dangereux de tirer une conclusion définitive.

Ce raisonnement est fondamental pour éviter des décisions basées sur des données biaisées, ce qui arrive bien plus souvent qu’on ne le pense.

Première approche avec des données concrètes

Prenons un jeu de données très simple. Supposons que vous mesuriez le temps de chargement d’une page avant et après une optimisation.

Version A : 2,8 s, 3,1 s, 2,9 s, 3,0 s, 2,7 s
Version B : 2,1 s, 2,2 s, 2,0 s, 2,3 s, 2,1 s

À l’œil nu, la version B semble clairement plus rapide. Les valeurs sont plus basses, mais surtout beaucoup plus regroupées. C’est exactement ce que cherche à mesurer la loi de Fisher : une différence claire et une faible dispersion.

Dans ce cas, la séparation est forte. Même sans calcul complexe, votre intuition rejoint le raisonnement statistique.

Des formations informatique pour tous !

Débutant ou curieux ? Apprenez le développement web, le référencement, le webmarketing, la bureautique, à maîtriser vos appareils Apple et bien plus encore…

Formateur indépendant, professionnel du web depuis 2006, je vous accompagne pas à pas et en cours particulier, que vous soyez débutant ou que vous souhaitiez progresser. En visio, à votre rythme, et toujours avec pédagogie.

Découvrez mes formations Qui suis-je ?

Traduire la loi de Fisher en logique de développeur

En tant que développeur web, vous n’allez pas forcément appliquer la loi de Fisher à la main. En revanche, vous allez souvent implémenter des outils ou des scripts qui suivent ce raisonnement.

L’idée centrale peut se résumer ainsi : ne jamais comparer deux résultats sans tenir compte de leur stabilité.

Cette logique s’applique à énormément de situations. Temps de chargement, taux de clic, taux de conversion, score utilisateur, performance d’un algorithme ou même résultats d’un moteur de recherche interne.

À chaque fois que vous manipulez des moyennes, la loi de Fisher vous rappelle qu’il faut aussi regarder la dispersion des données.

Exemple simple en JavaScript

Voyons maintenant comment traduire cette idée dans du code, avec un exemple volontairement simple et accessible. Imaginons que vous ayez deux tableaux de valeurs représentant un indicateur mesuré sur deux versions différentes d’une fonctionnalité.

const versionA = [45, 50, 47, 49, 46];
const versionB = [38, 37, 39, 36, 38];

La première étape consiste à calculer la moyenne de chaque groupe.

function moyenne(valeurs) {
  const somme = valeurs.reduce((acc, val) => acc + val, 0);
  return somme / valeurs.length;
}

const moyenneA = moyenne(versionA);
const moyenneB = moyenne(versionB);

console.log(moyenneA, moyenneB);

À ce stade, vous avez déjà une première comparaison. Mais la loi de Fisher vous incite à aller plus loin.

Comprendre la notion de dispersion

La dispersion mesure à quel point les valeurs s’éloignent de la moyenne. En statistique, on utilise souvent la variance ou l’écart-type. Sans entrer dans des calculs complexes, retenez simplement que plus la dispersion est élevée, moins les résultats sont stables.

Voici une fonction simple pour calculer la variance :

function variance(valeurs) {
  const moy = moyenne(valeurs);
  const ecarts = valeurs.map(val => Math.pow(val - moy, 2));
  return moyenne(ecarts);
}

const varianceA = variance(versionA);
const varianceB = variance(versionB);

console.log(varianceA, varianceB);

Même si vous ne comprenez pas encore tous les détails mathématiques, ce code illustre un point clé : la loi de Fisher compare la différence entre les moyennes par rapport à la dispersion.

Supposons que la différence entre les moyennes soit faible mais que les variances soient très élevées. Dans ce cas, la loi de Fisher indique que la séparation est faible. Autrement dit, les groupes se mélangent trop pour conclure efficacement.

À l’inverse, une différence modérée entre les moyennes avec une faible variance peut être beaucoup plus significative. C’est souvent contre-intuitif, et c’est justement là que la loi de Fisher apporte une vraie valeur.

Pourquoi cette approche est précieuse en développement web

Le web moderne est rempli de données. Chaque clic, chaque chargement, chaque interaction produit une information mesurable. Le danger n’est pas le manque de données, mais leur mauvaise interprétation.

La loi de Fisher agit comme un garde-fou. Elle vous oblige à ralentir, à analyser, et à éviter les conclusions hâtives. Pour un développeur, cette posture est extrêmement précieuse, surtout lorsqu’il s’agit d’optimiser une application ou de justifier des choix techniques.

La loi de Fisher et les performances web

L’un des domaines où la loi de Fisher est la plus utile, sans qu’on le réalise toujours, concerne les performances. Temps de chargement, temps de réponse serveur, durée d’exécution d’un script JavaScript… tous ces indicateurs sont rarement stables.

Supposons que vous optimisiez une page en compressant des images ou en modifiant une requête API. Après déploiement, vous mesurez les performances avant et après. Vous constatez une amélioration moyenne de 100 millisecondes. Sur le papier, cela semble positif. Pourtant, la loi de Fisher vous invite à aller plus loin.

Si les temps de chargement varient énormément selon les connexions, les appareils ou l’heure de la journée, cette amélioration moyenne peut être trompeuse. En revanche, si les nouvelles mesures sont non seulement plus rapides, mais aussi plus régulières, alors l’optimisation est réellement efficace.

Autrement dit, la loi de Fisher vous apprend à valoriser la stabilité autant que la rapidité.

Exemple concret : mesurer un temps de chargement

Imaginons que vous mesuriez le temps de chargement d’une page en JavaScript à l’aide de l’API Performance du navigateur. Vous récupérez plusieurs mesures avant et après une optimisation.

const avant = [1200, 1350, 1100, 1600, 1250];
const apres = [980, 1000, 1020, 990, 1010];

La moyenne après optimisation est plus basse, mais surtout, les valeurs sont beaucoup plus proches les unes des autres. C’est exactement ce que la loi de Fisher considère comme une bonne séparation.

Même si la différence de moyenne n’est pas spectaculaire, la faible dispersion rend la conclusion beaucoup plus fiable.

La loi de Fisher et l’expérience utilisateur

L’expérience utilisateur, souvent abrégée en UX, est un autre terrain de jeu idéal pour la loi de Fisher. Les comportements humains sont par nature variables, parfois imprévisibles. Pourtant, les décisions UX sont souvent prises à partir de chiffres.

Prenons l’exemple du temps passé sur une page. Vous testez deux mises en page différentes. La première affiche une moyenne de 2 minutes, la seconde 2 minutes et 15 secondes. Là encore, la tentation est grande de choisir la seconde.

Mais si les utilisateurs de la première version passent tous entre 1 minute 50 et 2 minutes 10, tandis que ceux de la seconde oscillent entre 10 secondes et 5 minutes, la lecture change complètement. La loi de Fisher vous pousse à reconnaître que la seconde version est peut-être moins prévisible, donc moins fiable.

En développement web, cette nuance est essentielle. Une expérience légèrement moins performante mais stable est souvent préférable à une expérience très variable.

Application à un système de score ou de notation

De nombreux sites web utilisent des scores. Cela peut être un score de pertinence, un score de recommandation ou même une note attribuée à un contenu. Là encore, la loi de Fisher intervient en arrière-plan.

Imaginons un algorithme qui attribue un score à des articles en fonction du comportement des utilisateurs. Deux algorithmes sont testés. Le premier produit des scores très dispersés, le second des scores plus resserrés mais légèrement inférieurs en moyenne.

Grâce à la loi de Fisher, vous comprenez que le second algorithme est peut-être plus fiable. Il discrimine mieux les contenus sans produire de résultats extrêmes difficiles à interpréter.

Cette approche est très courante dans les systèmes modernes, même si elle est rarement expliquée aussi clairement.

Implémenter un indicateur inspiré de Fisher

Sans implémenter la formule exacte de la loi de Fisher, vous pouvez vous en inspirer pour créer des indicateurs simples et utiles.

Par exemple, vous pouvez comparer deux résultats en divisant la différence de moyenne par la somme des variances. Cela donne une mesure intuitive de la séparation.

function scoreSeparation(groupeA, groupeB) {
  const diffMoyenne = Math.abs(moyenne(groupeA) - moyenne(groupeB));
  const dispersion = variance(groupeA) + variance(groupeB);
  return diffMoyenne / dispersion;
}

console.log(scoreSeparation(versionA, versionB));

Ce score n’est pas une implémentation académique parfaite, mais il traduit très bien l’esprit de la loi de Fisher. Plus le score est élevé, plus la séparation est nette et exploitable.

Pour un développeur débutant, ce type d’approche est souvent plus utile qu’une formule mathématique complexe.

Quand on débute en développement web, on a tendance à chercher des réponses simples à des problèmes complexes. Un chiffre, une moyenne, un pourcentage semblent rassurants. Pourtant, le réel est presque toujours plus nuancé.

La loi de Fisher vous apprend une posture mentale. Elle vous incite à douter intelligemment, à analyser les données avec recul et à éviter les conclusions rapides. Cette compétence dépasse largement les mathématiques. Elle touche à la qualité de vos décisions techniques.

C’est aussi pour cette raison que ce concept reste pertinent, même si vous n’êtes pas spécialiste en statistiques.

Les limites à connaître

La loi de Fisher n’est pas une baguette magique. Elle repose sur des hypothèses, notamment sur la distribution des données. Dans certains cas, elle peut être moins pertinente ou nécessiter d’autres outils complémentaires.

En développement web, elle doit être vue comme un outil d’aide à la réflexion, pas comme une vérité absolue. Elle vous donne un angle de lecture supplémentaire, pas une réponse définitive.

La loi de Fisher montre que les mathématiques ne sont pas là pour compliquer le développement web, mais pour l’éclairer. Derrière ce concept statistique se cache une idée profondément humaine : apprendre à distinguer le signal du bruit.

En comprenant ce principe, vous gagnez en maturité technique. Vous apprenez à interpréter les données avec nuance, à valoriser la stabilité autant que la performance et à prendre des décisions plus solides dans vos projets web.

À mesure que vos applications grandissent et que les données s’accumulent, cette façon de penser devient un véritable allié. La loi de Fisher ne vous demande pas de devenir statisticien. Elle vous invite simplement à devenir un développeur plus conscient, plus rigoureux et, finalement, plus serein face aux chiffres.

C’est souvent à ce moment-là que l’on réalise que les mathématiques, loin d’être un obstacle, peuvent devenir un formidable levier de compréhension et d’amélioration continue.

Alban

Fondateur de l’agence Créa-troyes, affiliée France Num
Intervenant en Freelance.
Contactez-moi

crea-troyes.fr